The basics of software coupling metrics and concepts

The difference between coupling and cohesion

For many, the differences between coupling and cohesion may appear somewhat murky. However, they each represent two distinctly different concepts that guide software design, and it's important to understand the role of each.

Coupling metrics focus on the number of dependencies between the components of an application. Tightly coupled application architectures contain prohibitively immutable dependency connections. If the applications and services do not require frequent updates and changes, these types of architectures are generally easy to manage. However, tight coupling makes it extremely complex to develop, test, deploy and manage components independently.

Contrary to coupling, cohesion references the degree to which the components of an application share methods and data in common. A cohesive module contains tightly interrelated code, but the fact that components can share common methods and data without knowledge of each other leads to a decrease in direct dependencies. As such, many teams aim to achieve high architecture cohesion and low coupling.

What are coupling metrics?

Software coupling metrics help development teams determine the complexity of their architecture based on the dependencies between classes, modules and methods. These metrics reveal how the components in an application are connected, the strength of their dependencies and the stability of the overall design.

Tight coupling makes it difficult to alter a single component without causing direct changes to others. Updates, tests and even refactoring are all complicated by tight coupling. A system becomes loosely coupled if individual components require little or no knowledge of the surrounding components to operate. As such, teams can build distributed applications with components that can act and evolve independently.

Created by researchers Norman Fenton and Austin Melton, the Fenton and Melton metric is commonly used to measure the degree of an architecture's coupling. The following formula calculates the level of coupling, C, between components a and b:

C(a, b) = i + n / (n + 1)

In this formula, the variable n represents the actual number of direct dependencies that exist between components a and b. The variable i will produce a value that indicates the level of coupling that exists between a and b. Developers can determine i by examining each of those components and identifying the tightest dependency relationship, with 0 representing the lowest level of dependency and 5 representing the highest.

Efferent and afferent coupling

To accurately calculate degrees of coupling, software teams must also delineate the nature of a component's dependency relationships. There are two major types of software coupling that are necessary to identify: efferent and afferent.

Efferent coupling is a measure of how many components a given class, module or method depends on to operate. A sizable level of efferent coupling indicates that a component may be difficult to observe, reuse, test and maintain. For instance, it's unlikely that development teams will be able to update a class with a great deal of efferent coupling without also updating each class it depends on. In most cases, teams will want to decompose these dependencies, which will help instill the single responsibility principle associated with object-oriented design.

Alternatively, afferent coupling gauges the number of components that are dependent on a particular class, module or method. While it still may make a component difficult to change, high afferent coupling is not necessarily a bad thing, as it can invariably occur in certain pieces of code, such as an application's core framework. However, it is a poor architecture practice to maintain extensive afferent coupling across a large number of applications. Ideally, a component with bundles of afferent coupling should remain small and take on as few responsibilities as possible.

In Figure 1, we illustrate the efferent coupling (Ce) and the afferent coupling (Ca) of a particular class, Class A.

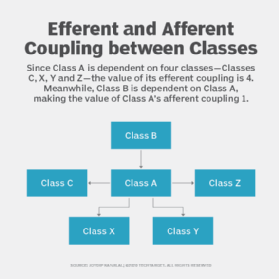
As the diagram shows, Class A is dependent on four other classes - C, X, Y, and Z. Meanwhile, there is a single class - Class B - that depends on Class A. In this case, the efferent coupling of Class A has a value of 4, while the value of its afferent coupling is 1.

Instability

Instability is a metric used to measure the relative susceptibility of a component to breaking changes. Instability indicates that a software class, package, subsystem or other given module will be significantly impacted by changes elsewhere.

Instability is calculated according to the following formula, where I is denoted by instability:

I = Ce / (Ce + Ca)

This formula will produce a value for I that ranges from 0 to 1. Components are considered to be generally stable when this calculation places the value of I closer to 0. Components with tighter coupling will usually produce a value closer to 1, which indicates that it is highly susceptible to breaking changes.

Using the example class from earlier, we can calculate the instability of Class A by:

I = 4 / (4 + 1)

Hence, the instability of Class A is 0.8, indicating that it is particularly susceptible to breaking changes. While the class is not completely incapable of independent changes, it still maintains enough dependencies to prohibit modularity.

Abstractness

A large part of reducing tight coupling and creating a modular architecture revolves around abstracting application components to increase their independence. The degree of abstraction that exists in an architecture is given by the number of abstract classes in a module or a component. This is a ratio of the number of abstract components, such as classes and application interfaces, to the total number of components.

This metric also ranges from 0 to 1. A value of 0 indicates a completely non-abstracted component, while 1 indicates complete abstraction. The number of abstract classes in a component or module is denoted by Ta and the number of concrete classes by Tc. The degree of abstraction, A, is given by:

A = Ta / (Ta + Tc)