What is a quantum circuit? Quantum vs. classical circuit

How quantum circuits work

Quantum circuits use logic gates to perform complex calculations on quantum particles, with measurements producing the final results. Since qubits are extremely fragile and vulnerable to noise that could distort results, quantum logic gates are built to limit the steps qubits must go through and still keep their quantum states coherent.

The process begins by preparing a qubit, which then passes through a series of quantum gates that manipulate the qubit's quantum state, guiding its behavior at each step of the computation. The final step is a measurement gate, which collapses the qubit's superposition -- its ability to be in multiple states simultaneously -- into a definite classical bit value of 0 or 1.

This output can be used for various applications, such as solving problems too complex even for supercomputers, simulating complex systems or potentially breaking certain cryptographic codes.

These are the most important gates:

• Initialization gate. This gate, represented by |0> in quantum notation, inputs the qubits.
• Superposition (Hadamard) gate. The Hadamard gate, represented by H in quantum notation, takes a qubit that's in a definite 0 or 1 state and flips it into a state that represents both 0 and 1 simultaneously.
• Switching (Pauli-X or X-) gate. This gate switches 0 to 1 and 1 to 0.
• Rotating (phase) gate, or P-gate. The phase gate rotates the vector representing a qubit's state around the z-axis by a specified amount. Vectors are geometric objects used to represent quantum states and typically have several axes, such as x, y and z.
• Entanglement (CNOT) gate. The CNOT gate is conditional. If qubit 0's state equals 1, the gate applies that same status to its qubit pair, enabling both qubits to be entangled. Quantum entanglement enables researchers to explore multiple solutions at the same time.
• Final (measurement) gate. This gate produces a probabilistic output, transforming the quantum state into algorithms for classical computing. One such algorithm is Shor's algorithm, which is used for factoring extremely large numbers and is particularly useful in cryptography.

Quantum circuits can be designed for a single qubit or for multiple qubits.

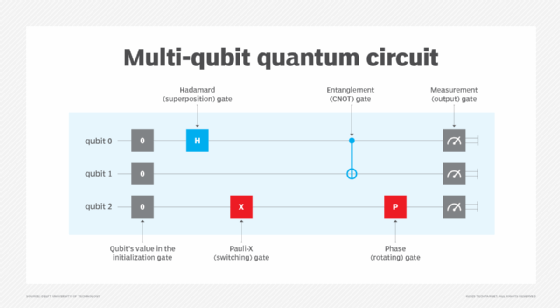
The diagram of a multi-qubit circuit in Figure 1 uses standard quantum notation for indicating qubits, gates and operations. Gates usually appear as boxes, except for CNOT gates, which appear as vertical lines. The first row of the diagram, reading from left to right, shows an initialization gate, a Hadamard gate (H) that puts the qubit in superposition and a meter-like symbol to represent the measurement gate that provides the output. In the second row of the diagram, a CNOT gate creates entanglement if the first qubit is in the 1 state, followed by the measurement gate. The third line shows a Pauli-X gate that flips the qubit to the opposite of its value at input (0 or 1), a phase gate (P) that rotates the vector representing the qubit's state and, finally, the measurement gate.

Quantum circuit simulators, such as IBM's Qiskit and Google's Cirq, provide visual tools to create and view similar diagrams of quantum circuits.

Example 1: Quantum circuit for 1 qubit

Scenario. Experimentalists want to make sure their single qubit works correctly:

1. They begin with a qubit in state |0>, which is like the regular 0 bit in classical computing.
2. They apply a Hadamard gate (H), which puts the qubit into superposition, meaning it's both 0 and 1 at the same time. In other words, there's a 50% chance of getting 0 and a 50% chance of getting 1.
3. They measure the qubit, which consequently collapses into a definite value of either 0 or 1.

Summary

In this circuit, scientists started with one qubit, inserted a superposition gate and measured the result. By running the circuit many times and checking the results, they can see if their qubit is truly random or if it's biased toward heads or tails in the figurative coin flip. The simple test helps them understand and improve this basic quantum building block.

Example 2: Designing a quantum circuit for multi-qubits

Scenario. Researchers need to find a specific item in an unsorted database. A search using classical computers would take weeks if not months, but using Grover's algorithm -- a quantum algorithm designed to take advantage of quantum computing's search advantages -- they can reduce the time to minutes:

1. Scientists start with two qubits in the state |0>.
2. They use Hadamard gates on each qubit to create superposition.
3. They apply a CNOT gate so the first qubit controls the second, and another CNOT so the second controls the third. This creates entanglement between the qubits.
4. The scientists measure the final state of the qubits, which collapses the superposition and gives a definite outcome of 0 or 1.

Summary

In this circuit, scientists started with two qubits, created superposition, added entanglement and measured the result. Each step involved specific gates, and the outcome depended on the operations performed.

How quantum circuits are used

Quantum mechanics operates on two fundamentals: superposition and entanglement. Superposition enables qubits to exist in multiple states simultaneously, while entanglement means qubits can share the same characteristics at the same time, regardless of the distance between them. These properties enable scientists to solve many more problems than previously thought possible.

Innovations enabled by quantum computing include the following:

1. Quantum simulation. Researchers can model complex systems in fields such as finance, chemistry and materials science, driving breakthroughs in financial modeling, drug discovery and the development of new materials. One example of this is how JPMorganChase uses quantum circuits to improve Monte Carlo simulations, a mathematical technique to assess risk. By using quantum circuits to rapidly process huge amounts of data and variables, the company can gain deeper insights into market dynamics to help clients make more informed investment decisions.
2. Quantum communication and networking. In traditional cryptography, parties exchange keys to encrypt and decrypt information. Quantum key distribution (QKD) perfectly secures data transmissions from bad actors by using the principle of entanglement; any variation during transmission indicates potential hacking. For example, Switzerland-based ID Quantique offers quantum-safe cryptography and QKD products to businesses and governments seeking enhanced data security.
3. Quantum cloud computing. In the cloud, the quantum attributes of superposition and entanglement can solve specific problems much faster and more accurately than even supercomputers. For example, Google's Sycamore quantum computer, accessible via the cloud, can process the same information in a little over six seconds that it would take the world's fastest supercomputer, HPE's El Capitan, several decades to complete.
4. Advancements in quantum algorithms. These include potential speedups in machine learning, particularly for pattern recognition and classification tasks, with applications in optimizing logistics processes, such as traffic flow. For example, Volkswagen uses quantum circuits to optimize traffic flow in urban areas, demonstrating significant reductions in congestion and travel time.
5. Quantum sensing. This technology uses entanglement to detect extremely faint signals or subtle changes in things like magnetic fields, gravity or even biological processes, which can produce much more precise measurements than possible with regular sensors. For example, Q-Ctrl, an Australia-based vendor, claims its software enhances quantum sensors, enabling more accurate measurements in such areas as navigation, environmental monitoring and medical imaging.

Comparing quantum circuits vs. classical circuits

Classical circuits can perform calculations on physical phenomena that researchers can observe and measure. The 0s and 1s of binary logic yield definite results.

In contrast, quantum circuits operate on microscopic particles that are challenging to observe and only take on concrete form when measured, which results in probabilistic outcomes. The quantum properties of superposition and entanglement also enable quantum computers to process vast amounts of data, potentially producing significantly faster computation for specific types of problems.

Figure 2 summarizes the main differences between classical and quantum circuits.

History of quantum circuits

The history of quantum circuits began in the 1980s when physicist David Deutsch proposed the concept of a universal quantum computer and introduced the quantum circuit model as a tool for computing quantum algorithms. In his 1985 paper, "Quantum theory, the Church-Turing principle and the universal quantum computer," Deutsch described the quantum circuit as a sequence of quantum gates acting on qubits, comparing it to the classical circuit that operates on bits.

In the 1990s, important algorithms, including Shor's for factoring incredibly large numbers and Grover's for rapidly searching unsorted databases, highlighted the potential by showing how quantum computers could solve certain complex problems more efficiently than even supercomputers can. Researchers then designed quantum gates to manipulate qubits; in the late 1990s and early 2000s, experimentalists, including Dave Wineland, demonstrated how quantum circuits could be used to perform complex calculations by manipulating ions.

Since then, the field has evolved rapidly, with industry experts working on increasing numbers of qubits, improving coherence times and developing more sophisticated quantum algorithms and programming tools -- e.g., the quantum approximate optimization algorithm (QAOA) and the variational quantum eigensolver (VQE).

More recently, cloud-based programming tools, such as Qiskit and Cirq, have helped to democratize access to quantum computing by lowering the barrier to entry, fostering wider participation in the field.

Future of quantum technology and applications

Quantum technology has impacted nearly every field, enabling researchers to make unprecedented discoveries in cryptography, computing, materials science, medicine and navigation. Experts in energy management use quantum technology to improve grid management and optimize renewable energy, while the aerospace industry uses quantum simulations for safer, more efficient aircraft designs. As quantum circuits become more accessible, smaller companies can gain access to advanced computational resources, fostering innovation and leveling the playing field.

Progress is driven by collaboration among physicists, computer scientists, engineers and experts in industry sectors who work together to accelerate advancements in quantum circuit technology. One notable example is the European Quantum Industry Consortium that partners with industry, academia and government stakeholders to share best practices, establish standards and address key challenges in quantum computing across sectors.

Current research focuses on addressing errors and decoherence, such as keeping qubits free from external noise and interference that can lead to errors in computation, as well as issues of scalability, including expanding quantum networks while maintaining interconnectivity and coherence.

In the long run, collaboration and persistent research could help scientists build a fault-tolerant quantum circuit, which is essential for more reliable, large-scale quantum computing.

Leah Zitter, Ph.D., is a seasoned writer and researcher on generative AI, drawing on over a decade of experience in emerging technologies to deliver insights on innovation, applications and industry trends.