tree structure

What is a tree structure?

A tree data structure is an algorithm for placing and locating files (called records or keys) in a database. The algorithm finds data by repeatedly making choices at decision points called nodes.

A node can have as few as two branches (also called children) or as many as several dozen. Although the tree structure's composition is straightforward, in terms of the number of nodes and children, a tree can be gigantic and complex.

Advantage of a tree structure

A tree structure consists of nodes connected by edges. One of its significant advantages over other data structures such as arrays, linked lists, stacks and queues is that it is a non-linear data structure that provides easier and quicker access to data. While linear data structures store data sequentially, tree structures permit data access in different directions.

As data sizes increase, access in such structures becomes slower, which can be hugely problematic in today's hyper-digital world. Tree structures can avoid such issues.

Tree structure properties

A tree can contain one special node called the "root" with zero or many subtrees. It may also contain no nodes at all. Every edge directly or indirectly originates from the root. The tree is always drawn upside-down, which means the root appears at the top. One parent node can have many children, but every child node has only one parent node. The maximum number of children per node is called the tree "order.".

In a tree, records are stored in locations called "leaves." The name indicates that records always exist at endpoints; there is nothing beyond them. Not every leaf contains a record, but more than half do. A leaf that does not contain data is called a "null." The maximum number of access operations required to reach the desired record is called the "depth."

The only way to perform any operation on a tree is by reaching the specific node. For this, a tree traversal algorithm is required.

Balanced and unbalanced trees

If the order is the same at every node and the depth is the same for every record, the tree is said to be balanced. Other trees have varying numbers of children per node, and different records might lie at different depths. In this case, the tree is said to have an unbalanced or asymmetrical structure.

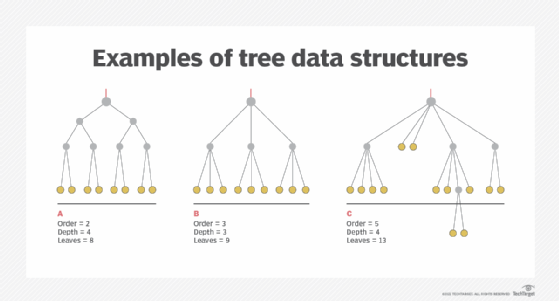
This illustration shows three examples of tree structures. Structures A and B are balanced, and structure C is unbalanced.

The key elements in each tree are as follows:

• Roots are at the top and represented by red lines
• Nodes are gray dots
• Children are solid gray lines
• Leaves are at the bottom and represented by gold dots

As the process moves away from the root and toward the leaves, children can branch out from a node. However, children never merge into a node.

A practical tree can have thousands, millions or billions of nodes, children, leaves and records. The trees shown here are simple enough to be rendered in two dimensions, but with some large databases, three dimensions are needed to clearly depict the tree structure.

Tree structure terms

Common terms associated with tree structures include:

• Node: An entity containing a key or value
  • Almost all nodes have pointers to child nodes
  • External nodes do not link to child nodes
• Root: The node at the top of the tree
  • There is always only one root per tree
• Internal node: Any node that has at least one child node
  • Also called inner node or branch node
• External node: The last nodes of each path
  • Also called outer node, terminal node or leaf node
• Edge: The link between two nodes
• Degree of a node: The total number of branches of that node
• Height of a node: The length of the longest downward path from the node to a leaf node
• Depth of a node: The number of edges from the root to the node
• Parent: Any node (except the root node) with one edge upward to a node
• Child: The node below a parent node connected by its edge downward
• Subtree: The descendants of a node
• Height of the tree: The height of the root node or the depth of the deepest node
• Forest: A collection of disjoint trees

Different types of tree structures

A general tree is a data structure with no constraints on the hierarchical structure. This means that a node can have any number of children. This tree is used to store hierarchical data, such as folder structures.

Other common tree structures are:

• Binary tree: In a binary tree structure, a node can have at most two child nodes, known as the left child and right child.
• Adelson-Velsky and Landis (AVL) tree: An AVL tree is a self-balancing tree, in which each node maintains a value called the balance factor, which refers to the height difference between the left and right subtree. For each node, the balance factor is either -1,0 or 1.
• B-tree: A b-tree is a self-balancing search tree, in which nodes can contain more than one key and two or more children.
• Binary search tree: The node's left child must always have a value less than or equal to the parent's value. Further, the right child must always have value more than or equal to the parent's value.
• Splay tree: A splay tree structure refers to a self-balancing binary search tree that gets rearranged (or "splayed") so that recently accessed elements can be quickly accessed again.
• T-tree: A self-balancing tree structure optimized for databases that keeps both data and index in memory.
• Heap tree: When every parent node's accompanying key value is larger or equivalent to the key values of any of their children's key values.
• Trie: Pronounced “try” and derived from the word “retrieval,” a trie tree structure stores and organizes strings as data items in a visual graph. Trie is also referred to as a keyword tree.

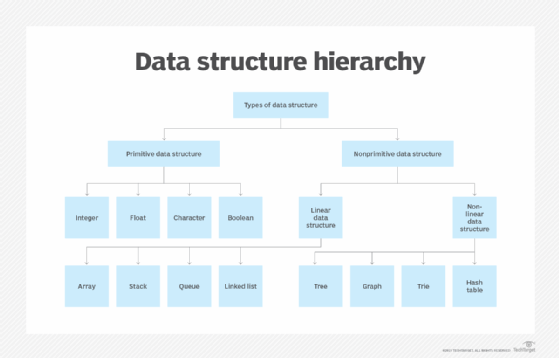
Applications of tree structures

Popular applications of tree structures include:

• Tree structures are also used to easily identify the presence of an element in a set.
• A binary search tree, which is a more constricted extension of a binary tree, is used to implement sorting algorithms, and in search applications in which data is constantly entering and leaving.
• Compilers use binary trees to build syntax trees and store router tables in routers.
• Most popular databases use B-trees and T-trees to store data.
• B-trees are used in database indexing to speed up search and in file systems to implement directories.
• A heap tree is used to perform a sorting operation called heap sort.
• A trie data structure is used in modern routers to store routing information.

Check out essential big data best practices for businesses and how to improve data quality.