Mobile Security and Privacy
In this excerpt from chapter 11 of Mobile Security and Privacy, authors Raymond Choo and Man Ho Au discuss privacy and anonymity in terms of mathematics.

The following is an excerpt from Mobile Security and Privacy by authors Raymond Choo and Man Ho Au and published by Syngress. This section from chapter 11 explores differential privacy and anonymity.
Anonymity refers to the absence of identifying information of an individual. In the digital age, user anonymity is critically important since computers could be used to infer individuals' lifestyles, habits, whereabouts, and associations from data collected in different daily transactions. However, merely removing explicit identifiers may not provide sufficient protection. The preliminary reason is that the released information, when combined with publicly available information, can also reveal the identity of an individual. A famous example is the Netflix crowdsourcing competition. In 2012, Netflix released a data set of users and their movie ratings. People could download the data and search for patterns. The data contained a fake customer ID, together with movie, customer's rating of the movie and the date of the rating. It is claimed that since customer identifiers have been removed, the released information would not breach user privacy. However, Narayanan and Shmatikov showed how customers can be identified when the dataset from Netflix is combined with some auxiliary data (such as data from IMDB).
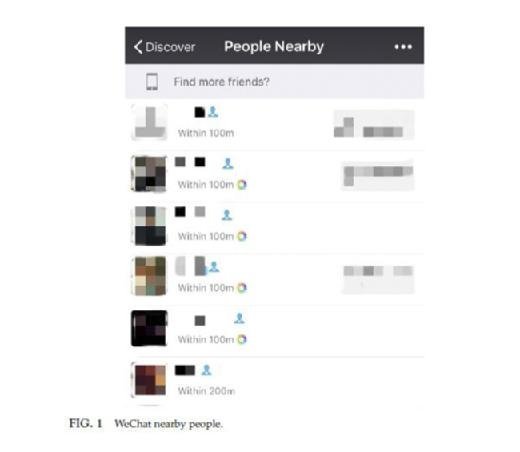
Location privacy is also of great concern in the mobile setting. Here we briefly review a case related to the location privacy of a location-based social network (LBSN), namely, WeChat, as discussed in (Wang et al., 2015). By using a fake GPS position and mobile phone emulation, it is possible to reveal the exact location of any WeChat user with the nearby service turned on (Fig. 1).
The previous example raises a question: what kind of information do we wish to protect when we talk about privacy protection? In other words, how do we define privacy? Traditional models in dealing with data confidentiality are not applicable in this case, since we have to maintain data utility. In the Netflix competition example, the data set is released to the public for mining, while in WeChat Nearby service, the user should be able to obtain the list of users nearby.
Over the years, the research community has developed various privacy models, including k-anonymity and differential privacy. In this chapter, we discuss these definitions and implications and the techniques to achieve them.
1.1 Organizations
This rest of this chapter is organized as follows. In Section 2, we present the definition of k-anonymity and discuss its practical implications. In Section 3, we discuss various techniques to achieve the definition. In Section 4, we discuss differential privacy, including its definition and implications. A differentially private mechanism that helps supporting differential privacy is reviewed in Section 5. We conclude in Section 6.
Definition of k-anonymity
k-anonymity, proposed by Sweeney, is a property of protecting released data from reidentification. It can be used, for example, when a private corporation such as a bank wants to release a version of data concerning clients' financial information to
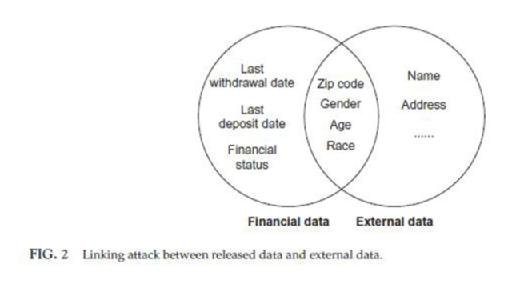
some public organizations for research purpose. Under this circumstance, released data should have the property that individual subjects of the data cannot be reidentified so as to protect their privacy. In other words, all the records in the released database should remain unlinkable to the clients. Clients' original data from a bank usually contains information such as name, address, and telephone number that can directly identify clients. One possible way to hide the identity is by directly removing the sensitive information from the database. However, it cannot guarantee clients' privacy. Information like zip code, gender, age and race, clients' identities still can be reidentified. Zip code provides an approximate location. Through searching by specific age, gender, and race, it is still possible to reveal clients' identities. Another possible way to achieve reidentification is called linking attack. Apart from attributes like name and address which can directly break the anonymity of data, there are also attributes called quasi-identifier (QID) which is used to link released data to external data. Gender, age, race and zip code is a typical tuple of QIDs and this tuple of QIDs from released data has high probability that also appears in some external data. If there are external tables like voter registration lists, then by linking the QIDs from released data to voter data, clients' identities may be revealed (Fig. 2).
Mobile Security and Privacy
Authors: Raymond Choo & Man Ho Au
Learn more about Mobile Security and Privacy from publisher Syngress
At checkout, use discount code PBTY25 for 25% off this and other Elsevier titles
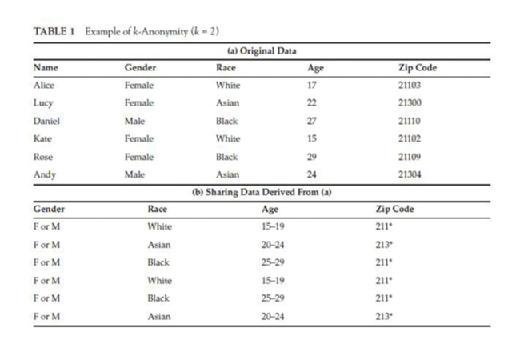
k-anonymity requires that in the released data, each record can be mapped to at least k records in the original data. In another words, each record from the released data will have at least k - 1 identical records in the same released data. For example in Table 1, (a) is the original data and (b) is the data derived from (a). (b) has k-anonymity where k = 2. In Sweeney (2002), Latanya Sweeney presented the principle of k-anonymity and proved that if the released data owns the property of k-anonymity, then the linking attack which links the released data to other external data and tries to break the data anonymity can be defended. Intuitively, this is because each record in released data will have at least k - 1 same records.
Mechanisms that support k-anonymity
After k-anonymity was proposed, various attempts had been made in designing a good algorithm that turns a database into a form that satisfied this definition. The main two techniques used to enforce k-anonymity in released data are generalization and suppression. Generalization consists of replacing attributes considered to be QIDs with a more general value. In Table 1, the values of gender, age, and zip code from (a) are all substituted by a generalized version in (b). Generalization can be applied in levels from a single cell to a tuple of attributes to achieve k-anonymity. Suppression consists of removing sensitive attributes to reduce the amount of generalization when achieving k-anonymity. Same as generalization, suppression can also be applied in cells or whole attributes. The combination of generalization and suppression has been used to construct different algorithms to help data satisfy k-anonymity. The conventional framework of such an algorithm always starts by suppressing several sensitive attributes and then partitions tuples of remaining attributes into groups and substituting accurate QIDs' values into generalized ones for each group, which are also called equivalent classes. This kind of generalization is homogeneous generalization and has been used to address k-anonymity in Iwuchukwu and Naughton (2007), Ghinita et al. (2007), and LeFevre et al. (2008). A property of homogeneous generalization is that if an original record ti matches the released record tj′ whose corresponding original record is tj, then tj also matches ti′. This property is called reciprocity. The most significant point for homogeneous generalization is how to divide the equivalent classes. The partitioning strategy will directly influence the utility of released data. There are two ways to do the partitioning job: global recording (full-domain anonymization) and local recording. Global recording means that within a column, the same generalization strategy is applied to the equal value. So if two tuples in the original data have identical QID values, then they must have the same released value. However, in local recording, two tuples with identical QID values may have different generalized values. Incognito algorithm proposed in LeFevre et al. (2005) uses dynamic programming and is shown to be outperformed by previous algorithms on two real-life databases. The main idea of Incognito is that any subset of the tuple of QIDs with k-anonymity should also have the property of k-anonymity. Mondrian algorithm presented in LeFevre et al. (2006) uses a strategy called multidimensional global recording. In Mondrian, each attribute in the dataset represents a dimension and each record represents a point in the space. Instead of partitioning each records, Mondrian algorithm partitions the space into several regions and in each region, there are at least k points.
Algorithms using local recording may guarantee more anonymity in specific situation.
Another generalization method is called nonhomogeneous generalization. For nonhomogeneous generalization, the property of reciprocity does not necessarily hold for all records. In Table 2, (b) is the released data derived from (a) using homogeneous generalization, and it is clear that (t1′, t2′, t5′) is an equivalent class and (t3′, t4′) is another . In an equivalent class, all the generalized QID values are the same. However, in a nonhomogeneous generalized table (c), t1′, t2′ and t5′ have different
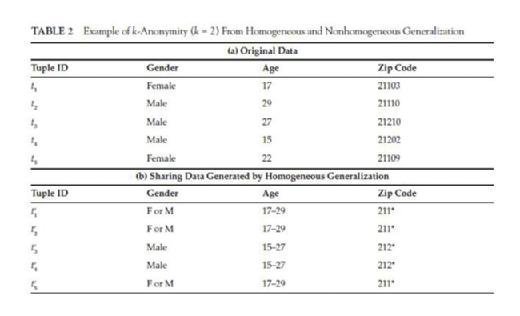
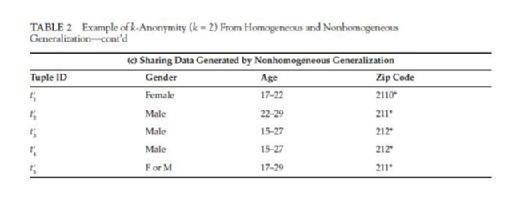
generalized QID values. While both table (b) and (c) have 2-anonymity, (c) offers higher data utility since the generalized QID ranges in (c) is either smaller or equivalent to the corresponding ones in (b). This illustrates that by using nonhomogeneous generalization, one may achieve a higher data utility on the released data.
In Wong et al.'s work, original data and released data are seen as a graph and records from data are vertices. To achieve k-anonymity, each vertex from the graph should have exactly k matches in the same graph including the vertex itself. If we consider a matching between two vertices as an edge, then the former sentence can be rewritten as each vertex in the graph should have out degree and in degree k. So in such graph, there are k disjoint assignments can be extracted and each assignment represents a correspondence between vertices. Even though Wong et al.'s work use nonhomogeneous generalization, there is still the requirement that the generalized graph should form a ring in their strategy which causes redundancy.
Read an excerpt
Download the PDF of chapter 11 in full to learn more!
Recently Doka et al. proposed a new algorithm called freeform generalization to implement k-anonymity in a nonhomogeneous way. They defined the problem as how to obtain high data utility in k-anonymity and wanted to solve this problem as an assignment problem in a bipartite graph that has two parts, namely, original and released. Each vertex from original part should have exactly k matches in the released part, and each vertex in the released part should also have k matches in the original part. Doka et al. (2015) proposed an approach to constructing the bipartite graph which contains k disjoint components. To construct such graph, the idea is choosing k different perfect matchings from all the possible matchings including the self-matching from original data to released data for vertices. After choosing, each vertex in the released graph should have k possible identities. The construction is secure since each disjoint assignment has the same probability 1/k to be the true one for an adversary. So, each time the adversary wants to find the identities of the released records, he/she will have k possible results. In the construction, each edge between two vertices will be assigned a weight based on Global Certainty Penalty (GCP). GCP is used to measure the information loss of matching an original record to a released record. The released data should keep k-anonymity and data utility. So when choosing the k perfect matchings, the total GCP should be kept as small as possible. Finally, a greedy algorithm was presented in Doka et al. (2015). The input to the greedy algorithm is a weighted completed bipartite graph G = (S, T, E), and the output is a perfect match with a total weight close to the minimum. S represents vertices in original data and T represents in released data. A successful running of the algorithm is called an iteration. In each iteration, the algorithm tries to find perfect matching from S to T with a low total weight. And the self-matching from original data to released data with zero GCP will be found out in the first iteration. After one iteration, all the selecting edges will be removed from the bipartite graph and all the weights (GCP) on the edges will be redefined. After k iterations, k disjoint perfect matchings with low GCP will be presented. The algorithm can be used in the real word for a practical value k and the complexity for all k iterations is O(kn2), where n is the number of records in the original data.
Differential privacy
Since the introduction of k-anonymity, weaknesses of it as a model have been discussed, and these weaknesses lead to the proposal of stronger models including ℓ-diversity, t-closeness, or β-likeness. In this chapter, we do not go into details of these definitions and refer interested readers to the respective papers. Informally speaking, the main weakness in k-anonymity is that it does not guarantee proper protection of the sensitive attributes. For example, from Table 1(b), an adversary can safely conclude that if a target user is of age from 20-29 living in a place with zip code starting with 211, the target user is an African American with high probability. Since in the table, only Asians and African Americans are of age from 20-29 and all the Asians' zip codes start with 213.
4.1 Overview
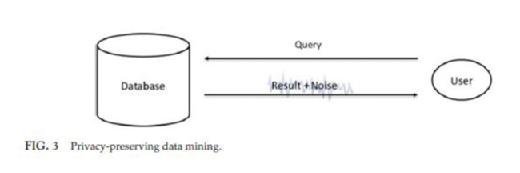
Differential privacy, introduced by Dwork (2006), is an attempt to define privacy from a different perspective. This seminal work consider the situation of privacy-preserving data mining in which there is a trusted curator who holds a private database D. The curator responses to queries issued by data analysts. Differential privacy guarantees that the query results are indistinguishable for two databases that differ only in one entry. From an individual point of view, it means that inclusion of one's information in the private database D would not cause noticeable changes in the observed query outcome; thus, privacy is protected. This is made possible via adding noise to the query result. The setting is shown in Fig. 3:
Note that it is possible to create a synthetic database by issuing a query that output the private database D, as discussed in Chen et al. (2011). However, as pointed out in Clifton and Tassa (2013), the utility of this synthetic database maybe too low for it to be useful.
4.2 Definition of Differential Privacy
Now we can recap the definition of differential privacy (Dwork, 2006). We first establish the notation. Let µ: D à R be a randomized algorithm with domain D and range R. In concrete terms, we can think of µ as a mechanism that answers a query to a database. Then we can formally define whether or not µ provides differential privacy as follows.
Definition 1. A randomized algorithm µ is ϵ-differentially private if for all possible subrange of µ, say S Ϲ R , and for all databases D1, D2 ∈ D that differs by only one record, the probability that µ gives the same output on input D1 and D2 with similar probability. More formally,
Pr(µ (D1) ∈ S) ≤ ee Pr(µ (D2) ∈ S).
Here ϵ controls how much information is leaked. For a small ϵ, the answer given by mechanism
µ on two databases that differ by one record is very likely to be the same. In other words, whether or not an individual's information is included in the database would not affect the outcome of the query significantly.
Example. Suppose the query we would like to make is whether or not Alice is a smoker. Consider mechanism µ defined as follows. µ first flips a fair coin b ∈ {0, 1}. If b = 0, return the true answer. Otherwise, flip another coin b′ = {0, 1}. If b′ = 0, return "yes," otherwise return "no." Now that there are two possible databases, namely, Alice is a smoker or Alice is not a smoker. If Alice is a smoker, µ output "yes" with probability 3/4 and "no" with probability 1/4. If Alice is not a smoker, µ output "yes" with probability 1/4 and "no" with probability 3/4. For any possible outcome, namely, "yes," or "no," the probability difference is at most three times. In other word, µ is (ln 3) differentially private.
Remarks. Perhaps one of the most useful properties of this definition is that differential privacy holds during composition. Suppose we have a database D. The data owner releases the query result µ 1(D). Later, he releases another query result µ 2(D). If µ 1 and µ 2 are ϵ1 and ϵ2 differentially private, the outcome of releasing both µ 1(D) and µ 2(D) is (ϵ1 + ϵ2) differentially private.
About the author:
Dr. Kim-Kwang Raymond Choo is a Fulbright Scholar and Senior Lecturer at the University of South Australia. He has (co)authored a number of publications in the areas of anti-money laundering, cyber and information security, and digital forensics. Dr. Choo was one of more than 20 international (and one of two Australian) experts consulted by the research team preparing McAfee's commissioned report entitled, "Virtual Criminology Report 2009: Virtually Here: The Age of Cyber Warfare"; and his opinions on cybercrime and cyber security are regularly published in the media. In 2009, he was named one of 10 Emerging Leaders in the Innovation category of The Weekend Australian Magazine / Microsoft's Next 100 series. He is also the recipient of several awards and has spoken at a number of industry conferences.
Dr. Man Ho Au is an assistant professor at the Hong Kong Polytechnic University. Before moving to Hong Kong, he has been a lecturer at the School of Computer Science and Software Engineering, University of Wollongong, Australia. His research expertise lies in information security and privacy. He has been an active member in the research community, having served as a program committee member of 15 international conferences in the last five years. He is also the program committee co-chair of the 8th International Conference on Network and System Security. Due to his excellent research track record, he has been appointed as the program committee co-chair of the 9th International Conference on Provable Security, to be held in Japan next year. He is an associate editor of Elsevier’s Journal of Information Security and Applications. He has served as a guest editor for various journals such as Elsevier’s Future Generation Computer Systems and Wiley’s Concurrency and Computation: Practice and Experience.







