CRC-4 (Cyclic Redundancy Check 4)
What is CRC-4 (Cyclic Redundancy Check 4)?
CRC-4 (Cyclic Redundancy Check 4) is a form of cyclic redundancy checking -- a method of checking for errors in transmitted data -- that is used on E1 trunk lines. CRC-4 is structured in a multi-frame consisting of 16 frames numbered 0 to 15. The CRC-4 multi-frame is then divided into two eight-frame sub multi-frames (SMFs) called SMF I and SMF II. Each SMF contains four CRC-4 bits designated C1, C2, C3 and C4.
Through multiplication and division processes, the CRC-4 bits sent in each SMF are compared to each other. If they match, the frame is considered error-free. Bit 1 is used for the CRC-4 bits.
Error detection in computer networks
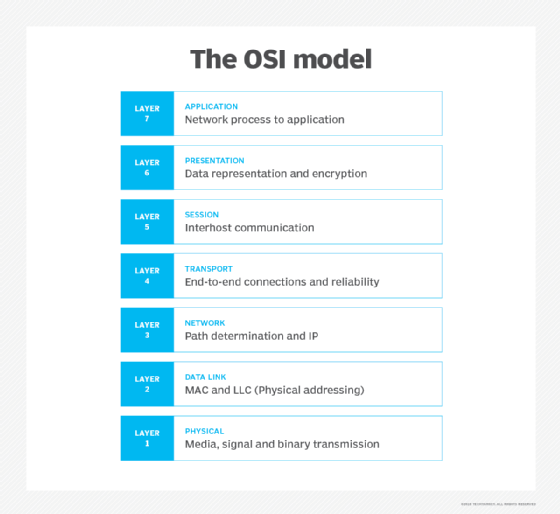
Computer networks use error detection techniques to verify if any data errors have occurred during transmission. This is done by adding an additional error detection code to a given message at either the data link layer (Layer 2) or transport layer (Layer 4) of the OSI (Open Systems Interconnection) model, which is a reference model for how applications communicate across a network.
An error is said to have occurred when there is a mismatch between the receiver's information and the sender's information. This usually happens when noise is introduced into the network as the data travels from the sender to the receiver. When an error occurs, a 0 bit may change to a 1, or vice versa.
The following are three of the most popular error detection methods.
Single parity check
This is a basic method that can detect simple errors by appending a redundant bit known as a parity bit at the end of the data unit to create an even number of ones. If the data block contains an odd number of ones, a 0 is added at the end.
Checksum
This is a slightly more complex method of error detection. Before a message is transmitted, a checksum byte is computed and appended to it. When the receiver gets the message, a new checksum is calculated and compared with the existing checksum. If there is a mismatch between the two checksums, it indicates an error. It they match, the message is assumed to be error-free.
Cyclic redundancy check
CRC is a hash function based on binary division. A sequence of redundant bits (called CRC bits) are appended to the end of the data block so that the resulting block is exactly divisible by a second, predetermined binary number. At the receiver's end, the incoming message is divided by this number. If there's no remainder, the message is considered error-free. A remainder indicates the presence of an error.
How does CRC-4 work?
CRC-4 uses a CRC code to verify the integrity of the framing sequence. It is structured in a multi-frame (MF) consisting of 16 frames numbered from 0 to 15. Each MF16 is split into two equal segments of eight frames, often called sub multi-frames SMF I and SMF II. SMF I consists of frames 0-7 and SMF II consists of frames 8-15.
In each SMF, the even frames place the CRC bits in the first bit position. These bits act as a CRC for the first sub multi-frame. The CRC bits in frames 8, 10, 12 and 14 act as the CRC for the second sub multi-frame. Since there are four CRC bits, this error detection method is known as CRC-4. All odd frames use the first bit position to indicate an error when detected by the CRC bits, which is flagged with an E-bit.
CRC-4 support is required for all network switches in Europe. Some ISDN signaling protocols use CRC-4 by default. Some older switches, including private branch exchanges (PBXs) and exchanges, do not support CRC-4. In this case, the exchange must either alter its configuration by turning its CRC-4 checking option on, or it must configure its firmware so the CRC-4 checking is off.
Mathematical representation of CRC-4
The CRC-4 error detecting code gets is name because the algorithm is based on cyclic codes. Also, the check value for data verification is a redundancy (i.e., it expands the message without adding any information).
Mathematically speaking, a 4-bit CRC applied to a data block of arbitrary length will detect any single error burst not longer than 4 bits, and a fraction 1 − 2−n of longer error bursts. Simply put, for a 4-bit CRC, the check value is 4. For this value, multiple CRCs are possible, each with a different polynomial.
To specify a CRC code and implement its algorithm, a "generator polynomial" is defined. Ideally, the polynomial should maximize the algorithm's error-detecting capabilities and minimize the overall collision probabilities. Its length, (i.e., the largest degree[exponent] +1 of any one term) is its most important attribute.
For a 4-bit CRC:
- Polynomial degree: n = 4
- Number of terms: n+1 = 5
- Bits required for encoding: n+1 = 5
There are three ways to express a polynomial as an integer: 0x3, 0xC and 0x9.
The first two are mirror images in binary, and represent the constants found in the code. The third is the number described by author Philip Koopman, a professor of electrical and computer engineering at Carnegie Mellon University and CTO of Edge Case Research.
So, for a polynomial, x4 + x + 1 may be transcribed as shown in Figure 2.









