
marrakeshh - Fotolia
IP subnetting: How to calculate subnet masks
Check out IP subnetting shortcuts on how to do subnet mask calculations and break down IP address classes to route traffic within your network.
Whether you need an IP subnetting cheat sheet or you're preparing for a Cisco Certified Network Associate, or CCNA, exam, this article shows you how to calculate a subnet mask, break down IP address classes and understand binary. If you're wondering how to figure out what subnet mask to use when you need X hosts and X networks, this tutorial is perfect for you. Take the interactive quiz at the bottom of this page to find out how much you've learned.
When you are going to take a CCNA exam, before the exam starts, write down the following public and private class address ranges, as well as the chart, because it will save you a lot of time and headaches.
IP address classes
Class A: 1 – 126 (127 reserved for loopback and diagnostic tests)
Class B: 128 – 191
Class C: 192 – 223
Class D: 224 – 239 (reserved, used primarily for IP multicasting)
Class E: 240 – 254 (reserved, experimental)
Private addresses
Class A: 10.0.0.0 through 10.255.255.255
Class B: 172.16.0.0 through 172.31.255.255
Class C: 192.168.0.0 through 192.168.255.255
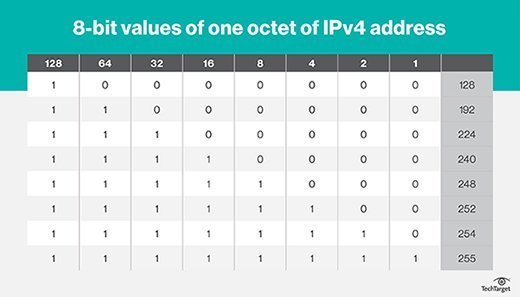
The chart above represents the 8-bit values of one octet of an IPv4 IP address. (See IPv6 subnetting resources sidebar.) If you add up all of the bits, it comes to 255, which is an all 1's mask.
If you are wondering how we get 256 in one octet, there is an implied zero at the end. If you are looking at a network, you can have a network address of 192.168.17.0. The modulus of 128 – 0 would be 256. To arrive at the subnet mask, we can do one of two things: Add the positive bits together, or take the least significant positive bit and subtract it from 256.
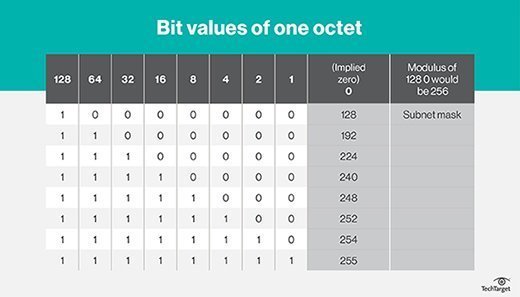
The chart comes in handy if you are being asked what the subnet mask would be for /27. You know the sum of the first three octets is 24, so you start counting 25 with the first bit -- 128. Counting to 27 would get you to the third most significant bit -- 32. Look to the subnet mask column, and you see it is .224.
A teacher of mine -- Jeremy Cioara, who has written several Cisco books -- told a story about a guy who owned a brick company. He had a lot of bricks, and people would come and buy them. As the guy got more successful, he had to figure out a way of putting the bricks in piles so it would be quick and easy to give customers the number of bricks they wanted.
To do that, he placed the bricks on pallets in the following quantities: 128, 64, 32, 16, 8, 4, 2 and 1. As a result, it was easy to come up with quantities for a customer. For example, if a customer wants 188 bricks, you would give him one of the 128-brick pallets. That would still leave the customer 60 bricks short of what was requested. To fill that gap, the company would provide the customer with four additional pallets: one with 32 bricks, one with 16, one with eight and one with four.
And here is the binary of 188:
128 64 32 16 8 4 2 1
1 0 1 1 1 1 0 0
Jeremy used this method to decide what subnet mask to use when you need X hosts and X networks.
Another teacher of mine used to do the 2ⁿ-2 table. But that's a little too complicated when you are going against time in a Cisco exam.
IPv6 subnetting resources
Expert information on how IPv6 changes subnetting
How IPv6 subnetting works in LAN and VLAN network design
IPv6 timeline for subnetting decision making
Sorting out IP subnetting networks and hosts
Here's how I determine networks or hosts. You know you have to subtract two, because you need one end for the network and one end for the broadcast address, or subnet mask. So, when you get to a bit value -- i.e., 128, 64, 32 and so on -- you subtract two, and the remainder will be the hosts.
Let's say you are told you have 57 hosts and are asked for the subnet mask. It's easy. You go to the chart and find that 57 is more than 32, but less than 64. Try to think 30 and 62 because you are thinking hosts. You would use the second bit, 64. So, if you go to the right side for the subnet mask, it would be .192.
If you are asked for valid hosts in the 192.168.30.7/28 range, you begin by counting off the chart to see the numerical value for the 28th bit, which is 16. Then, take a look at the last octet -- since 28 puts us in the last octet range -- and divide it by 16. In this case, we don't have to, because we can see it is less than 16, but if you are given .189 rather than .7, you would divide 189 by 16 and see it was over 11. Then, multiply 11 times 16 to see the first address in that subnet, 176. Then, add 16 to 176, and you'll get the first address of the next subnet, 192. That means .189 falls in the subnet 176 – 188. We know the first number is the network address, 192.168.30.176, and the last number is the broadcast address, 255.255.255.188. Remember, we are breaking down that 256 block, so we can't use the full 256 subnet -- only the portion blocking our network. That means the hosts must fall in the range of 177 – 187 -- one after 176 and one before 188.
Going back to our question of valid hosts in the 192.168.30.7/28 range, they would be:
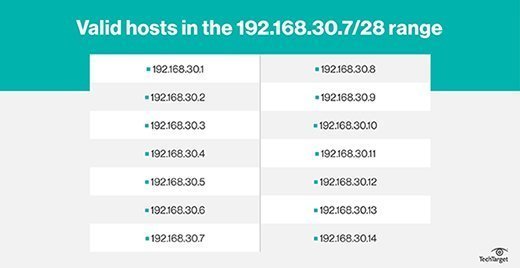
There are 14 hosts. Remember, the 2ⁿ-2 formula: The bit value minus 2 -- one for network and one for broadcast address or subnet mask -- equals the number you can use for hosts.
If you want to know how many of these 16-bit networks we can get out of that third octet, divide 256 by 16. The answer is 16. Don't slip and think the number of networks you can get is the bit value -- it just works out that way with /28. For a /26, you can get four networks -- 0 – 63; 64 – 127; 128 – 191 and 192 – 255. I didn't use the number 256 because I started at zero; the modulus -- value of 256 -- comes from zero to 255.
Here's another way to figure out how many 16-bit networks you can get out of an octet. If you take a look at our bit values of 128, 64, 32, 16, 8, 4, 2 and 1, double the number of networks per bit value starting with 2 for 128. You would then have 4 for 64, 8 for 32, 16 for 16, 32 for 8, 64 for 4 and 128 for 2. This is easier than dividing 256 by 16 to see that you can have 16 networks.
If you are get a problem asking for the subnet mask of 172.16.64.0/18, go back to the chart. And when you start counting at the first bit -- 128 -- think of it as being in the third octet, rather than the forth octet, so /18 would be the second bit -- 64 -- and the subnet mask for IP subnetting would be .192.
If you are asked how many hosts you would have, the calculation is easy. You've noticed the bit values are cut in half for descending order, so you just double them for ascending. Start with your most significant bit of the last octet -- 128 -- and multiply it by two to come up with the bit value of the least significant bit of the third octet and keep doubling:
| /17 |
/18 |
/19 |
/20 |
/21 |
/22 |
/23 |
/24 |
/25 |
/26 |
etc. |
| 32768 |
16384 |
8192 |
4096 |
2048 |
1024 |
512 |
256 |
128 |
64 |
etc. |
On a /18 network, you would have 16382 hosts (16384 -- 2).
That's the theory of my easy way to do subnetting. Here are some sample quiz questions.





