binary

What is binary?

Binary describes a numbering scheme in which there are only two possible values for each digit -- 0 or 1 -- and is the basis for all binary code used in computing systems. These systems use this code to understand operational instructions and user input and to present a relevant output to the user.

The term binary also refers to any digital encoding/decoding system in which there are exactly two possible states. In digital data memory, storage, processing and communications, the 0 and 1 values are sometimes called low and high, respectively. In transistors, 1 refers to a flow of electricity, while 0 represents no flow of electricity.

Binary explained

The binary numbering system was refined in the 17th century by Gottfried Leibniz. In mathematics and in computing systems, a binary digit, or bit, is the smallest unit of data. Each bit has a single value of either 1 or 0, which means it can't take on any other value.

Computers can represent numbers using binary code in the form of digital 1s and 0s inside the central processing unit (CPU) and RAM. These digital numbers are electrical signals that are either on or off inside the CPU or RAM.

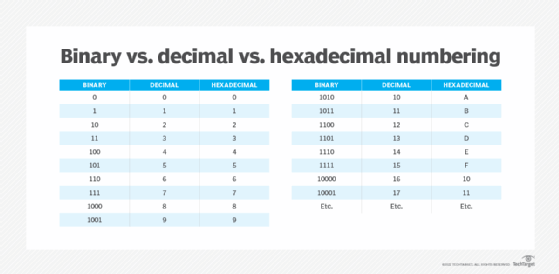
Binary vs. decimal

Since the binary system uses only two digits or bits and represents numbers using varying patterns of 1s and 0s, it is known as a base-2 system. Here, 1 refers to "on" or "true," while 0 refers to "off" or "false."

In contrast, the decimal numbering system is a base-10 system, where each possible place in a number can be one of 10 digits (0-9). In a multidigit number, the rightmost digit is in the first place, the digit next to it on the left is in 10th place, the digit further left is in 100th place and so on.

Example

In the four-digit number 1,980, here are the places occupied by each digit.

The importance of binary code

The binary number system is the base of all computing systems and operations. It enables devices to store, access and manipulate all types of information directed to and from the CPU or memory. This makes it possible to develop applications that enable users to do the following:

• view websites;
• create and update documents;
• play games;
• view streaming video and other kinds of graphical information;
• access software; and
• perform calculations and data analyses.

The binary schema of digital 1s and 0s offers a simple and elegant way for computers to work. It also offers an efficient way to control logic circuits and to detect an electrical signal's true (1) and false (0) states.

How binary numbers work

The binary system is the primary language of computing systems. Inside these systems, a binary number consists of a series of eight bits. This series is known as a byte. In the binary schema, the position of each digit determines its decimal value. Thus, by understanding the position of each bit, a binary number can be converted into a decimal number.

In decimal numbers, each additional place is multiplied by 10 as we move from right to left (first place, 10th place, 100th place, etc.). But, in binary numbers, each additional place while moving from right to left is multiplied by two. The two examples below explain this idea.

Example 1

Here's how the decimal values are calculated for an 8-bit (byte) binary number 01101000.

In this number, the first digit is at the far right, while the eighth digit is at the far left. The second (0) to the seventh (1) digits are read from right to left.

As the bit position increases from one to eight, the previous decimal value is multiplied by two. That's why the first bit has a value of 1, the second bit has a value of 2, the third bit has a value of 4 and so on.

The final value of the decimal number is calculated by adding the individual values from the above table. However, only those values where the bit equals 1 should be added. These values represent the "on" position. The 0s represent the "off" position, so they are not counted in the decimal value calculation.

So, for the binary number 01101000, the decimal value is calculated as the following:

8 + 32 + 64 = 104

Example 2

Here's how the decimal values are calculated for the binary number 11111111.

In this binary number, every bit has a value of 1, so all the individual values are added.

So, for this number, the decimal value is the following:

1 + 2 + 4 + 8 + 16+ 32 + 64 +128 = 255

Representing decimal numbers in binary format

As mentioned earlier, the binary numbering system only works with 1s and 0s. However, the position of just these two digits can represent many more numbers. The examples in the previous section show how any decimal number from 0 to 255 can be represented using binary numbers. Numbers larger than 255 can also be represented by adding more bits to an 8-bit binary number.

Here are the decimal numbers from zero to 20 and their binary equivalents.

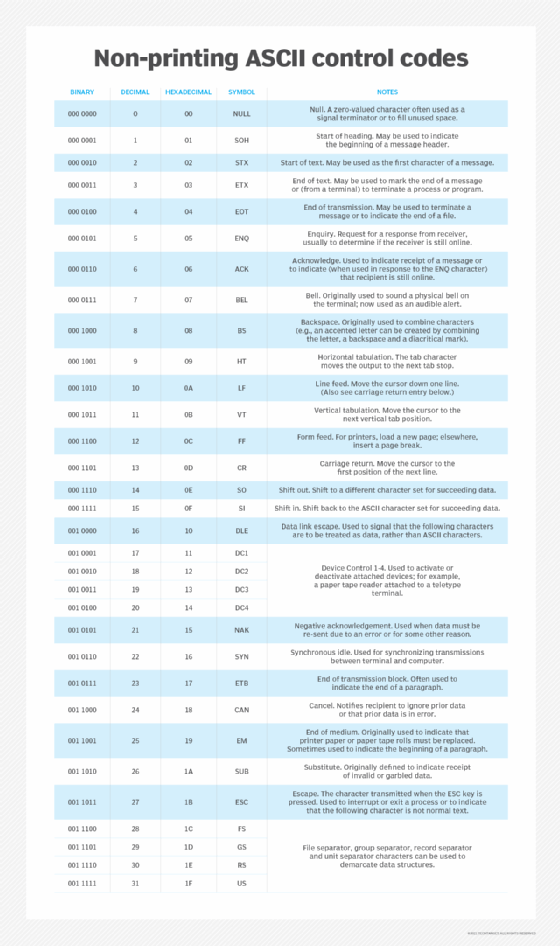
Converting binary numbers into text characters

Binary numbers can be translated into text characters using American Standard Code for Information Interchange (ASCII) codes to store information in the computer's RAM or CPU. ASCII-capable applications, like word processors, can read text information from the RAM or CPU. They can also store text information that can then be retrieved by the user at a later time. ASCII codes are stored in the ASCII table, which consists of 128 text or special characters. Each character has an associated decimal value.

In the first example of the previous section, the binary number is 01101000 (decimal number 104). In ASCII, this number would produce lowercase h. To form words, more letters need to be added to h. In binary terms, this means adding more binary numbers to the binary number for h.

Example

The binary code for ASCII lowercase i is 01101001. So, to create the word hi, the binary number for i is added to the binary number for h. This yields the following binary number:

01101000 + 01101001 = 0110100001101001

In decimal terms, the decimal numbers for h and i are 104 and 105, respectively.

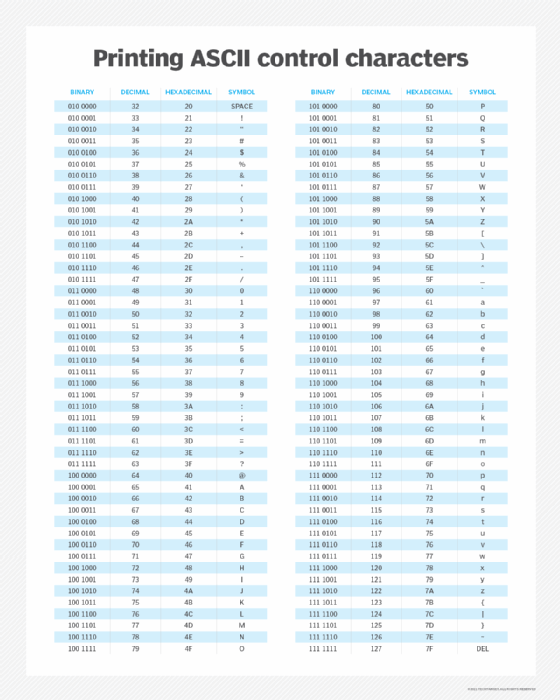
Other common examples of binary numbers converted to ASCII text code are the following.

See also: ASCII symbols; kibi, mebi, gibi, tebi, pebi and exbi; encoding and decoding; most significant bit or byte; and Extended Binary Coded Decimal Interchange Code.