binary-coded decimal
What is binary-coded decimal?
Binary-coded decimal is a system of writing numerals that assigns a four-digit binary code to each digit 0 through 9 in a decimal (base 10) number. Simply put, binary-coded decimal is a way to convert decimal numbers into their binary equivalents. However, binary-coded decimal is not the same as simple binary representation.
More about binary-coded decimal
In binary-coded decimal, each digit in a decimal base 10 number is represented as a group of four binary digits, or bits. Any base 10 number or digit can be represented in binary notation using binary-coded decimal.
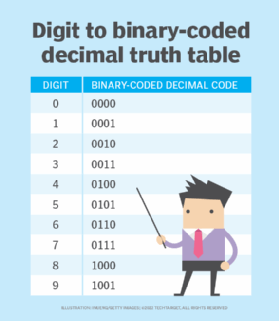
Each digit is encoded separately. The full number is first segregated into its individual digits. These digits are then represented by their equivalent 4-bit binary-coded decimal codes as shown in this truth table.
In general, decimal-to-binary encoding using binary-coded decimal can be done using either 4-bit or 8-bit equivalents. However, the 4-bit equivalent is usually preferred, which effectively represents the decimal values from 0 to 9.
Arithmetic operations, like multiplication and addition, are required to convert real binary numbers to decimal. However, in binary-coded decimal, only 10 different combinations are possible (see above table) in each 4-bit binary sequence. This makes binary-coded decimal an easier way to represent decimal numbers.
The following numbers are not considered binary-coded decimal: 1010, 1011, 1100, 1101, 1110 and 1111.
Representing larger digits and numbers with binary-coded decimal
In the decimal system, all numbers larger than 9 have two or more digits. In the binary-coded decimal system, these numbers are expressed digit by digit.
Example 1
Decimal number = 1764
The binary-coded decimal rendition is represented as the following:
| 1 |
7 |
6 |
4 |
| 0001 |
0111 |
0110 |
0100 |
Example 2
Decimal number = 238
The binary-coded decimal rendition is represented as the following:
| 2 |
3 |
8 |
| 0010 |
0010 |
0010 |
Example 3
Decimal number = 1895
The binary-coded decimal rendition is represented as the following:
| 1 |
8 |
9 |
5 |
| 0001 |
1000 |
1001 |
0101 |
The binary-coded decimal representation of a number is not the same as its simple binary representation. For example, in binary form, the decimal quantity 1895 appears as 11101100111. In binary-coded decimal, it appears as 0001100010010101.
The binary equivalents for each of the above examples always go from left to right. Other bit patterns are sometimes used in binary-coded decimal format to represent special characters relevant to a particular system, such as sign (positive or negative), error condition or overflow condition.
Advantages and applications of binary-coded decimal
The binary-coded decimal system provides a way to get around the size limitations imposed on integer arithmetic. It also enables easy conversion between machine-readable and human-readable numerals. Compared to the binary system, it is easy to code and decode binary-coded decimal numbers. Thus, binary-coded decimal offers a fast and efficient system to convert decimal numbers into binary numbers.
Binary-coded decimal is useful in digital displays, where it can be difficult to manipulate or display large numbers. Since binary-coded decimal treats each digit as a separate subcircuit, data manipulation in such devices becomes easier. Integrated circuits that are configured to give a binary-coded decimal output on such displays are available.
The binary-coded decimal conversion system is also used in some currency applications where floating point representations are not completely accurate.
Limitations of binary-coded decimal
Despite its advantages, binary-coded decimal comes with certain limitations. For example, representing a decimal number as binary-coded decimal requires extra bits of storage in a computer's memory, making it an inefficient way to store numbers. It also takes increased circuit complexity when compared to the standard binary system. Binary-coded decimal code can also be wasteful since many 4-bit states (10 to 16) are not used.
Another limitation of binary-coded decimal is that performing arithmetic tasks using binary-coded decimal numbers can be cumbersome since no digit can exceed 9. Consequently, adding of two decimal digits in binary-coded decimal could create a carry bit of 1, which must be added to the next group of 4 bits to arrive at the correct binary-coded decimal representation.
Types of binary-coded decimal
There are two types of binary-coded decimal.
Unpacked binary-coded decimal
In unpacked binary-coded decimal numbers, each 4-bit binary-coded decimal group is stored in a separate register inside a computer. The drawback here is that, if the registers are 8 bits or wider, space is wasted storing the binary-coded decimal numbers.
Packed binary-coded decimal
In packed binary-coded decimal numbers, a single 8-bit register stores two binary-coded decimal digits. By shifting the number in the upper register to the left four times and then adding the numbers in the upper and lower registers, the process combines two binary-coded decimal digits, which enables storage in a single register.
Binary-coded decimal vs. simple binary representation
In simple binary representation, the whole number is converted into its binary form by dividing the number by 2 repeatedly. In binary-coded decimal, each individual digit is converted to binary. The 4-bit binary equivalent of each digit is then written together.
Here's an example:
- The decimal number is 234.
- In binary format, 234 = 11101010
- In binary-coded decimal, 234 is written as the following:
- 2 = 0010, 3 = 0011, 4 = 0100
- Hence, 234 = 001000110100
See also: Extended Binary Coded Decimal Interchange Code, encoding and decoding, hexadecimal, big-endian and little-endian, globally unique identifier, universally unique identifier and American Standard Code for Information Interchange.
