International Data Encryption Algorithm (IDEA)

What is the International Data Encryption Algorithm (IDEA)?

The International Data Encryption Algorithm (IDEA) is a symmetric key block cipher encryption algorithm designed to encrypt text to an unreadable format for transmission via the internet. It uses a typical block size of 128 bits and takes 64 bits as an input, i.e., 64-bit data. IDEA performs 8.5 identical encryption and decryption rounds using six different subkeys. It uses four keys for output transformation.

First published in 1991 to replace the Data Encryption Standard (DES), IDEA was originally called Proposed Encryption Standard. The name was changed to Improved Proposed Encryption Standard and eventually to IDEA.

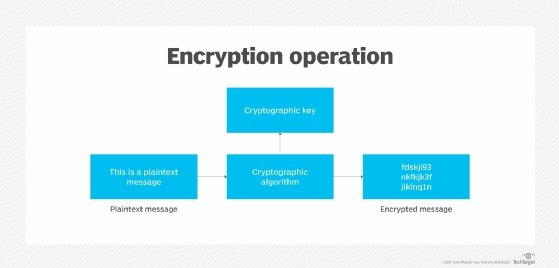
Understanding IDEA

IDEA was developed at ETH, a research university in Zurich, Switzerland, and is generally considered to be secure. The IDEA cipher encrypts text with the assumption that security in IDEA is not predicated on keeping the algorithm a secret, but rather on ignorance of the secret key.

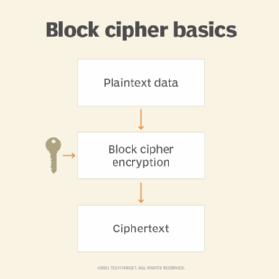
IDEA uses a 128-bit key and operates on 64-bit blocks. Essentially, it encrypts a 64-bit block of plaintext into a 64-bit block of ciphertext. This input plaintext block is divided into four subblocks of 16 bits each. It consists of a series of eight identical transformations, where each transformation is known as a round, as well as an output transformation, which is known as a half-round. Similar to the 16-bit plaintext block, the ciphertext block is also the exact same size.

A block cipher operates in round blocks, with part of the encryption key, known as round key, applied to each round, followed by other mathematical operations. After a certain number of rounds, the ciphertext for that block is generated.

Encryption in IDEA

IDEA derives most of its security from multiple interleaved mathematical operations:

• modular addition
• modular multiplication
• bitwise exclusive-OR (XOR)

By using a 128-bit key, IDEA encrypts a 64-bit block of plaintext into a 64-bit block of ciphertext. One process partitions the plaintext block into four 16-bit subblocks for each of the eight complete rounds, namely X1, X2, X3 and X4.

Another process produces six 16-bit key subblocks for each of the encryption rounds, namely Z1, Z2, Z3, Z4, Z5 and Z6. For subsequent output transformation, a further four 16-bit key subblocks are required. Thus, from a 128-bit key, a total of 52 16-bit subblocks are generated.

In each complete round, three algebraic operations are performed: bitwise XOR, addition modulo 2¹⁶ and multiplication modulo 2¹⁶+1.

The 14 steps for a complete round are the following:

1. Multiply X1 with Z1.
2. Add X2 to Z2.
3. Add X3 to Z3.
4. Multiply X4 with Z4.
5. Bitwise XOR the results of steps 1 and 3.
6. Bitwise XOR the results of steps 2 and 4.
7. Multiply the result of step 5 with Z5.
8. Add the results of steps 6 and 7.
9. Multiply the result of step 8 with Z6.
10. Add the results of steps 7 and 9.
11. Bitwise XOR the results of steps 1 and 9.
12. Bitwise XOR the results of steps 3 and 9.
13. Bitwise XOR the results of steps 2 and 10.
14. Bitwise XOR the results of steps 4 and 10.

Six subkeys are used in each of the eight rounds, and the final 4 subkeys are used in the ninth half-round final transformation.

Swapping occurs for every round until the final complete round (round 8). After eight complete rounds, the final half-round transformation occurs. The steps involved are the following:

1. Multiply X1 with the first subkey.
2. Add X2 with the second subkey.
3. Add X3 with the third subkey.
4. Multiply X4 with the fourth subkey.

The concatenation of the four blocks is the encrypted output.

Decryption in IDEA

The decryption process uses the same steps as the encryption process. However, different 16-bit key subblocks are generated. Each of the 52 16-bit key subblocks used for decryption is the inverse of the key subblock used during encryption with respect to applied algebraic operations.

Also, these subblocks are used in reverse order during decryption. Decryption in IDEA works on the shoes and socks principle, i.e., the last encryption is the first to be removed.

Advantages and applications of IDEA

Although IDEA was originally meant to replace DES, it did not do so. Nonetheless, it was incorporated into Pretty Good Privacy, which indicates its reliability and security.

IDEA supports easy hardware and software implementation for quick execution. It can be easily embedded into encryption software to protect data transmission and storage in several real-world applications:

• financial services
• broadcasting
• government
• video conferencing
• audio and video for cable TV
• business TV
• voice over IP
• email via public networks
• smart cards

See also cryptology, asymmetric cryptography, strong cryptography, quantum cryptography, cryptosystem, cryptographic checksum, hashing, Rivest-Shamir-Adleman algorithm, stream cipher, private key, public key, session key and Advanced Encryption Standard.