linear regression

What is linear regression?

Linear regression identifies the relationship between the mean value of one variable and the corresponding values of one or more other variables. This can involve analyses such as estimating sales based on product prices or predicting crop yield based on rainfall. At a basic level, the term regression means to return to a former or less developed state.

Linear regression in machine learning builds on this fundamental concept to model the relationship between variables using various ML techniques to generate a regression line between variables such as sales rate and marketing spend. In practice, machine learning tends to be more useful when working with multiple variables, called multivariate regression, where the relationships between them require more complex regression coefficients.

Linear regression is a basic component in supervised learning. At its core, linear regression can help determine if one explanatory variable can provide value in predicting the outcome of the other. For example, does ad spending on one medium or another have any meaningful impact on sales?

In the most basic case, linear regression tries to predict the value of one variable, called the dependent variable, given another variable, called the independent variable. For example, if you were trying to predict sales rate based on advertising spend, sales would be the dependent variable, while ad spend would be the independent variable.

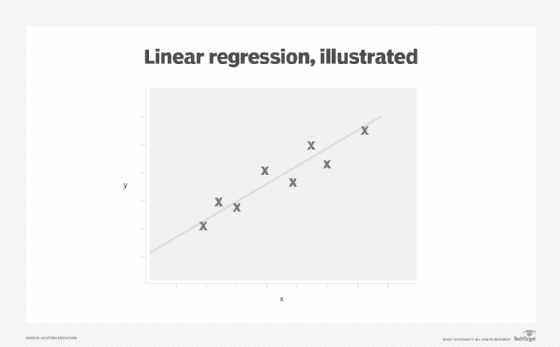
Linear regression is linear in that it guides the development of a function or model that fits a straight line to a graph of the data. This line also minimizes the difference between a predicted value for the dependent variable given the corresponding independent variable.

In the case of estimating sales rate, each dollar in sales might climb regularly within a certain range for every dollar spent on ads and then slow down once the ad market reaches a saturation point. In these cases, more complex functions need to be constructed using statistics or ML techniques to fit the data onto a straight line.

Why is linear regression important?

Linear regression is important for the following reasons:

• It works with unlabeled data.
• It is relatively simple and fast.
• It can be applied as a fundamental building block in business and science.
• It supports predictive analytics.
• It helps separate important relationships for further analysis or model development.
• It improves the accuracy of ML models for trend analysis.

Types of linear regression

There are three main types of linear regression.

Simple linear regression

Simple linear regression finds a function that maps data points to a straight line onto a graph of two variables.

Multiple linear regression

Multiple linear regression finds a function that maps data points to a straight line between one dependent variable, like ice cream sales, and a function of two or more independent variables, such as temperature and advertising spend.

Nonlinear regression

Nonlinear regression finds a function that fits two or more variables onto a curve rather than a straight line.

Examples of linear regression

Three common ways linear regression is used are the following:

1. Identifying the magnitude of the effect an independent variable, like temperature, might have on a dependent variable like ice cream sales.
2. Forecasting the impact of changes driven by the independent variable -- for example, how much more ice cream might be sold with different levels of advertising?
3. Predicting trends and future values -- like how much ice cream should be stocked to meet demand if the temperature is predicted to reach 90 degrees Fahrenheit?

Linear regression use cases

Typical use cases for linear regression in business include the following:

• Pricing elasticity. How much will sales drop if the price is increased by a given amount?
• Risk management. What is the anticipated liability for a given storm strength?
• Commodities futures. What is the relationship between rainfall and crop yield?
• Fraud detection. What is the probability of a transaction being fraudulent?
• Business analysis. How much could sales rise with various levels of profit-sharing incentives?

Advantages and disadvantages of linear regression

Advantages of linear regression include the following:

• It aids exploratory data analysis.
• It can identify relationships between variables.
• It is relatively straightforward to implement.

Disadvantages of linear regression include the following:

• It does not work well if the data is not truly independent.
• Machine learning linear regression is prone to underfitting that does not account for rare events.
• Outliers can skew the accuracy of linear regression models.

Key assumptions of linear regression

Linear regression requires the data set to support the following properties:

• Data needs to be organized as a continuous series, such as time, sales in dollars or advertising spend. It does not work directly with data that comes in the form of categories like days of the week or product type.
• Observations need to be truly independent of each other. For example, sales and profits might not be independent if the cost of goods or other factors do not affect profits separately.
• Data needs to be cleansed of any outliers.
• The amount each data point varies from the straight line needs to be consistent over changes in the independent variable, called homoscedasticity.

Linear regression vs. logistic regression

Linear regression is just one class of regression techniques for fitting numbers onto a graph.

Multivariate regression might fit data to a curve or a plane in a multidimensional graph representing the effects of multiple variables.

Logistic regression predicts whether a given data point belongs to one class or another, such as spam/not spam for an email filter or fraud/not fraud for a credit card authorizer.