Rijndael

What is Rijndael?

Rijndael (pronounced rain-dahl) is an Advanced Encryption Standard (AES) algorithm. It replaced the older and weaker Data Encryption Standard (DES) when it was selected as the standard symmetric key encryption algorithm by the National Institute of Standards and Technology (NIST).

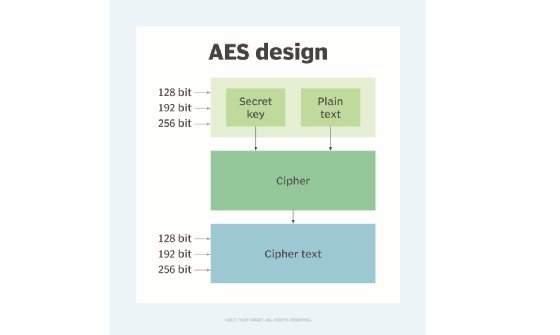
Rijndael is an iterated block cipher, meaning that it encrypts and decrypts a block of data by the iteration or round of a specific transformation. It supports encryption key sizes of 128, 192, and 256 bits and handles data in 128-bit blocks.

Rijndael as Advanced Encryption Standard

DES has been in use since 1977. However, by the early 2000s, it began to show security weaknesses. It became obvious that threat actors could use brute-force attacks and crack DES. A better and more secure algorithm was required to encrypt sensitive, unclassified federal information in the U.S. In 2001, NIST encouraged cryptographers to present a more resilient algorithm to replace DES to encrypt mission-critical data.

Five algorithms -- MARS, Rivest Cipher 6, Serpent, Twofish and Rijndael -- were presented.

Ultimately, NIST selected Rijndael as AES. Before confirming its selection, NIST evaluated Rijndael on several factors, including security, cost and implementation. Rijndael was chosen because it offered the best performance, security, efficiency, flexibility and ease of implementation. The NIST selection was formalized when Federal Information Processing Standards 197 was released.

AES is approved in the U.S. for use with government documents that require high-level security clearance.

Guiding principles of Rijndael

Rijndael is named after its two creators: Belgian cryptologists Vincent Rijmen and Joan Daemen. It has its origins in Square, another algorithm designed by the pair. This new algorithm improves upon Square based on three fundamental guiding principles:

1. It can resist all known attacks.
2. It ensures source code compactness and speed on multiple computing platforms.
3. It features a simple design.

Understanding Rijndael AES

Rijndael accepts input as one-dimensional 8-bit byte arrays that create data blocks. The plaintext input is mapped onto state bytes. The corresponding cipher key is also a one-dimensional 8-bit byte array. In the algorithm, different transformations occur sequentially on intermediate cipher results:

• Key and block size. Rijndael can operate in varying data blocks and key sizes of 128, 192 or 256 bits. There are 1,021 times more AES 128-bit keys than DES 56-bit keys.
• Subkey and key schedule. Rijndael's key schedule derives subkeys from the cipher key. The cipher key expands to create an expanded key, and the subkey is created by deriving a round key. To ensure security and protect the algorithm from cryptanalytic attacks against its key generation methods, the expanded key is never directly specified but is always derived from the cipher key.
• Whole byte operations. These operations include addition and multiplication within a finite field and with matrices. These bytes are treated as polynomials, simplifying implementations.

Key schedule in Rijndael

The key schedules differ depending on the length of the key in Rijndael.

Keys with 128-bit and 192-bit lengths

The subkey material consists of all the round keys in order, the original key and stretches. Each stretch consists of 4-byte words, which is the same length as the original key. Each word is the XOR of the preceding 4-byte word.

The first word in the stretch is rotated 1 byte to the left. This is followed by byte transformation using the S-box from the Byte Sub step and then a round-dependent constant that is XORed to the first byte.

Keys with 256-bit lengths

Here, the S-box from the Byte Sub step alone is applied to the word from the preceding stretch for the fifth word in a stretch.

Working of Rijndael

In Rijndael, encryption happens through a series of matrix transformations or rounds. The number of rounds are variable, depending on the key or block sizes used:

• 128 bits = 9 rounds
• 192 bits = 11 rounds
• 256 bits = 13 rounds

The Rijndael algorithm is based on byte-by-byte replacement, swap and XOR operations. The procedure is as follows:

• The algorithm generates 10 128-bit keys from the 128-bit key, which are stored in 4x4 tables.
• The plaintext is divided into 4x4 tables, each of 128-bit sizes.
• Each 128-bit plaintext piece goes through a variable number of rounds as mentioned above. The code is generated after the 10th round.

Each round consists of four steps:

1. Byte Sub. Each byte of the block is replaced by its substitute in the S-box.
2. Shift Row. In a block made of bytes 1 to 16, bytes are arranged in a rectangle and shifted according to block sizes.
3. Mix Column. Here, matrix multiplication is performed, where each column is multiplied by the matrix. The bytes being multiplied are treated as polynomials, not as numbers. When results have more than 8 bits, the extra bits are cancelled out by XORing the binary 9-bit string 100011011 with the result. This technique is similar to what is used in in cyclic redundancy checks.
4. Add Round Key. Here, the subkey for the current round is XORed.

When Rijndael is performed several times with different round keys, its security increases significantly.

Advantages and applications of Rijndael

Rijndael has a number of advantages over DES and Triple DES.

First, its block sizes can mirror those of their respective keys, which places this algorithm over the limits required for AES design conditions. It is also easy to implement with simple components and easily proven properties. Additionally, Rijndael works three times faster than DES in software. In Rijndael, it is possible to use 160- or 224-bit keys. The algorithm also supports block sizes of 160 or 224 bits. This enables greater flexibility in transformation rounds during encryption.

The Square block cipher on which Rijndael is based was vulnerable to several cyber attacks. Rijndael improves the security of this older algorithm by using alternating mix column and mix row transformations to resist such attacks. Since the key length can vary as desired, the algorithm is also secure for many real-world applications, especially when more transformation rounds are added.

That's why Rijndael is ideal for the secure exchange of keys and to transmit data with a length of 128 or 256 bits.

Compared to other algorithms that were candidates for AES, Rijndael provides strong security against the following:

• linear cryptanalysis
• differential cryptanalysis
• opportunistic attacks
• power attacks
• timing attacks

Rijndael also has low memory requirements, which makes it suitable for space-restricted environments. Its rich algebraic structure makes it possible to easily and quickly assess its security. Plus, it offers high efficiency and performance on many computing platforms and hardware and software environments, including the following:

• large arrays
• desktops
• laptops
• mobile devices
• smart cards

Drawbacks of Rijndael

Rijndael may be vulnerable to a type of attack called the square attack. But, in practical terms, this attack cannot compromise the security of the algorithm.

The algorithm is also limited by its inverse cipher that takes more code and cycles and is, therefore, not ideally suited for some implementations.

See also strong cryptography, quantum cryptography, cryptographic checksum and cryptosystem.