wave number

What is a wave number?

A wave number, or wavenumber, refers to the spatial frequency of a wave over a specific unit distance. The wave number is measured either in cycles per unit distance or in radians per unit distance, depending on the context. A wave number is related to but different from frequency, which is temporal in nature. Frequency refers to the number of wave cycles that pass through a given point in 1 second, with each cycle representing a unit of time rather than a unit of distance.

A wave number that is based on the number of cycles per unit distance is sometimes referred to as linear wave number, ordinary wave number, spatial wave number or spectroscopic wave number. In many cases, it is simply called wave number or wavenumber. The linear-based approach is used extensively in spectroscopy and chemistry.

A wave number based on radians is sometimes referred to as angular wave number or, to a lesser degree, circular wave number, although this type is also commonly called just wave number or wavenumber. The result has been a fair amount of confusion between the two types. Unfortunately, there is no clear standard or consensus for how to refer to either one, which can make it difficult to be certain which type is being referenced or used. Sometimes the only option is to view the underlying calculations.

Working with linear wave numbers

A linear wave number is often contrasted with wavelength, which is the distance between the same successive points on a wave, such as two consecutive wave crests. Wavelength is not concerned with the number of waves, only the length of each one.

However, a wave's wavelength is directly related to its wave number. In fact, a wave number is sometimes described as the number of wavelengths in a given distance. The wave number can also be defined as the reciprocal of the wavelength, as expressed through the following formula.

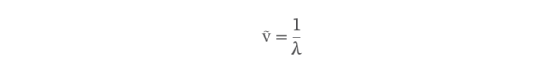
The wave number is represented by the Greek letter nu (ν) with a tilde over it, and the wavelength is represented by the Greek letter lambda (λ). The wavelength is typically specified in meters (m) or centimeters. The International System of Units defines wave number as simply m^-1 or 1/m.

If you know a wave's wavelength, you can calculate its wave number or vice versa. Because the two are in a reciprocal relationship, the wave number grows larger as the wavelength becomes shorter, and the wavelength grows longer as the wave number becomes smaller.

A linear wave number can also be described in terms of the wave's velocity (v) and frequency (f), as they relate to its wavelength. Velocity refers to the wave's speed and is measured in meters per second (m/s). Frequency refers to the number of wave cycles per second and is measured in hertz (Hz). The relationship between wavelength, velocity and frequency can be described by the following formula.

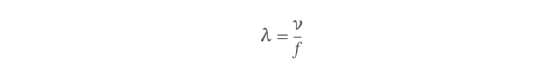
The formula states that wavelength is equal to velocity divided by frequency. When calculating the wave number for a specific wave, you can incorporate this formula into the linear wave number formula by replacing λ in the wave number formula with the velocity and frequency from the wavelength formula, as in the following equation.

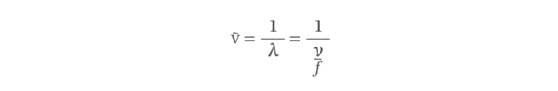
The equation starts with the linear wave number formula and then replaces the denominator based on the wavelength formula. From that point, you can then multiply both the numerator and denominator by f to arrive at your final equation.

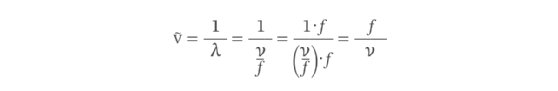
The results indicate that a wave number is equal to the wave's frequency divided by its velocity. The velocity used in these formulas will depend on the type of wave and environment in which it travels. For example, the speed of light in free space (vacuum) is approximately 2.99792 × 10⁸ m/s. However, the velocity of a sound wave traveling through water is less than 1,500 m/s. The lower the water's temperature, the lower the velocity.

Working with angular wave numbers

In physics, angular wave numbers are generally used rather than linear wave numbers. This means the wave number is measured in radians per unit time, not wave cycles. As a result, the wave number formula must be modified to take into account the differences in measurement and their relationship with angular frequency. The angular wave number is typically symbolized by k instead of ṽ, and the numerator is replaced with 2π to take into account the use of radians, resulting in the following formula.

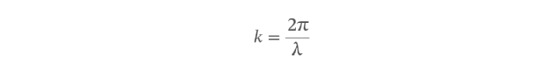
The 2π is used in the numerator because that is the number of radians in a circle (360 degrees), which is how a full wave cycle is represented when measured in radians -- 1 radian is equal to about 57.3 degrees. Despite the difference in formulas, calculating radian-based wave numbers works much like linear-based wave numbers. A reciprocal relationship still exists, so the wave number will grow larger as the wavelength becomes shorter or vice versa.

You can also take advantage of the relationship between velocity, frequency and wavelength when calculating radian-based wave numbers, again starting with the same wavelength formula.

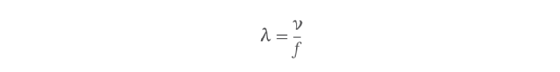
As with the linear wave number equation, you need only replace λ in the angular wave number formula with the velocity and frequency from the wavelength formula, as in the following equation.

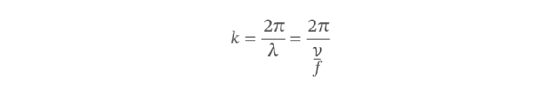
Also as before, you can then multiply both the numerator and denominator by f to simplify the formula.

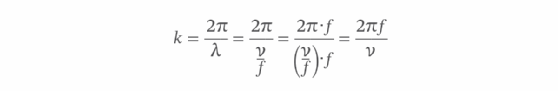
The equation now indicates that the angular wave number is equal to 2π times frequency divided by velocity. For the angular formula, however, you can take one more step. It turns out that 2πf is equal to the angular frequency, as symbolized by the Greek letter omega (ω), which you can use to simplify the formula even further.

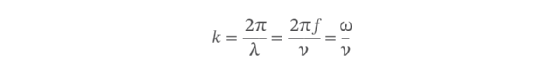
As the equation demonstrates, the angular wave number is equal to the angular frequency divided by the velocity, drawing a clear connection between the angular wave number and the wave's angular frequency.

See how multiphysics simulation could accelerate the advent of quantum computing -- and vice versa.