analog-to-digital conversion (ADC)
What is analog-to-digital conversion (ADC)?
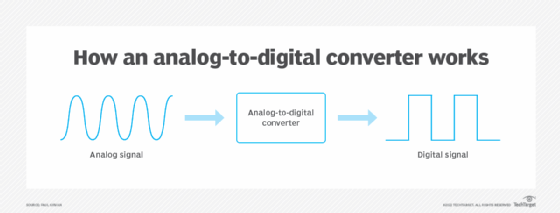
Analog-to-digital conversion (ADC) is an electronic process in which a continuously variable, or analog, signal is changed into a multilevel digital signal without altering its essential content.
An analog-to-digital converter changes an analog signal that's continuous in terms of both time and amplitude to a digital signal that's discrete in terms of both time and amplitude. The analog input to a converter consists of a voltage that varies among a theoretically infinite number of values. Examples are sine waves, the waveforms representing human speech and the signals from a conventional television camera.
The output of the analog-to-digital converter has defined levels or states. The number of states is almost always a power of two -- that is, 2, 4, 8, 16, etc. The simplest digital signals have only two states and are called binary. All whole numbers can be represented in binary form as strings of ones and zeros.
Why is digitization important?
Digital signals propagate more efficiently than analog signals, largely because digital impulses are well defined and orderly. They're also easier for electronic circuits to distinguish from noise, which is chaotic. That is the chief advantage of digital communication modes.
Computers "talk" and "think" in terms of binary digital data. While a microprocessor can analyze analog data, it must be converted into digital form for the computer to make sense of it.
A typical telephone modem makes use of ADC to convert the incoming audio from a twisted-pair line into signals the computer can understand. In a digital signal processing system, an analog-to-digital converter is required if the input signal is analog.
What is the Nyquist theorem and why is it important?
The Nyquist or sampling theorem describes analog-to-digital conversion. It enables the reproduction of a pure sine wave measurement, which is also known as the sample rate.
The way people experience the world is mostly analog; think sound and light waves. For these signals to be used in computing, they must be converted to digital ones. However, digital electronics works in discrete numbers. To convert an analog signal to a digital one, measurements must be sampled at a regular frequency. The sample rate must be at least twice its frequency. This approach is used in digital audio and video to reduce aliasing, or the production of a false frequency.
A sample rate that is too low won't accurately depict the original signal; it will be distorted or have aliasing when reproduced. A rate that is too high will use more storage and processing resources than necessary.
The Nyquist theorem is used to locate the point where the right amount of information is gathered. Other names for the theorem are the Nyquist-Shannon theorem or the Whittaker-Nyquist-Shannon sampling theorem.
How the Nyquist theorem works
Analog signal frequency is measured in hertz. Their frequency describes the number of times they go up and down in a second. Electrical engineer and mathematician Claude Shannon explained the theorem as follows: "If a function x(t) contains no frequencies higher than B hertz, it is completely determined by giving its ordinates at a series of points spaced 1/(2B) seconds apart."
To correctly reproduce a signal, the sample rate has to be two times the highest frequency.
To show how this works, imagine a sensor on the Earth tasked with measuring the brightness of the sky. It takes a measurement once a day, every 24 hours. Data from this sensor would lead a researcher to inaccurately believe the sky stays at a constant brightness throughout the day. If the experiment is changed so that measurements are taken 18 hours apart, it would produce equally inaccurate data, randomly alternating between full daylight, complete darkness and some dim light.
Have the sensor take a measurement every 12 hours, however, and the results depict the Earth's day-night cycle over a 24-hour period. To get an accurate measure of the Earth's 24-hour rotation, the measurements must be done at least twice its rate, which are 12-hour intervals.
Importance of analog-to-digital conversion
A key role ADC has played in modern technology development is the evolution of voice communication systems from old-style analog signal processing to today's voice over IP, or VoIP, systems. From the 1950s through the 1970s, telephone systems were unable to communicate directly with computers. The emergence of modems made it possible, but they were not always cost-effective.
For computer input devices, such as teletypewriters, to communicate with computer systems, they had to connect to a modem that linked to the front end of a computer system, such as a mainframe. Modem transmission speeds were slow compared with today's ultrahigh-speed networks. A fast modem in the 1960s and 1970s provided 2,400 bits per second of throughput to computers. By contrast, today's systems operate at gigabit speeds.
ADC technology became the linchpin for developing digital private branch exchange, or PBX, systems, as well as systems for smaller office applications. These systems used a fully digital switching architecture, and ADC units embedded in telephone sets -- and, sometimes, within the switch itself -- converted analog voice signals to digital bit streams that the digital switch could process.
Conversely, the opposite process was used when a voice call was delivered to another user. A digital-to-analog converter, or DAC, converted the digital code from the switch into audible analog signals. This model is still in use today, more than 50 years later. ADC technology is also used to process video signals into digital bit streams for transmitting visual images also with voice communications.
The future of analog-to-digital conversion
The nature of audible sounds generating sine waves that ADC units can sample is not going to change unless there is a quantum change in physics. As such, ADC technology is likely to be embedded in all types of computing devices long into the future. ADC is perhaps one of the most significant technological advancements of the past century.
Find out more about the future of digital transformation in the enterprise in our ultimate guide.
