logical equivalence
What is logical equivalence?
Logical equivalence is the condition of equality that exists between two statements or sentences in propositional logic or Boolean algebra. The relationship between the two statements translates verbally into "if and only if." In mathematics, logical equivalence is typically symbolized by a double arrow (⟺ or ⟷) or triple lines (≡). The double arrow is sometimes referred to as an IIF function.
This expression provides an example of logical equivalence between two simple statements:
A ∨ B ⟺ B ∨ A
The expression includes the statements A ∨ B and B ∨ A, which are connected together by the IIF function. Each statement uses the OR Boolean function (∨) to indicate an inclusive disjunction between variables A and B. This means that the statement returns a true value if either variable is true or if both variables are true, but it returns a false value if both variables are false. The expression in its entirety is effectively stating that the statement "variable A or variable B" is logically equivalent to the statement "variable B or variable A."
How is logical equivalence determined?
An expression's statements are considered logically equivalent if they return identical truth values for every row in a truth table. The truth table shown in Figure 1 reveals the truth values for the statements in the example expression given previously.
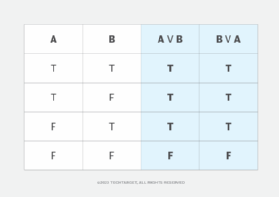
The table includes one column for each variable (A and B) and one row for each possible combination of true and false values for those variables. It also includes a column for each statement's evaluation based on the variable values. The statement columns are highlighted in blue for easy comparison.
The truth values in the statement columns are identical in all rows, so the statements are considered to be logically equivalent. However, if the second statement were changed from B ∨ A to B ∨ ¬A, the truth table would look somewhat different, as shown in Figure 2.
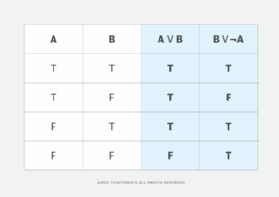
The modified statement (B ∨ ¬A) uses the NOT Boolean function (¬) to indicate a logical negation. This means that variable A returns true when it is false and returns false when it is true. As a result, the truth values in columns A ∨ B and B ∨ ¬A are no longer identical, so the statements are not logically equivalent.
A truth table can also be used for more complex statements when determining whether they are logically equivalent. For example, a truth table for the statements A ∨ (B ⋀ C) and (A ∨ B) ⋀ (A ∨ C) would include eight rows that map out the true/false combinations for variables A, B and C. It is shown in Figure 3.
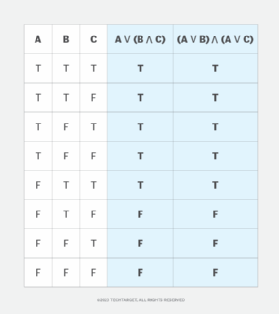
The statements shown in Figure 3 use both the OR Boolean function and the AND Boolean function (∨), which indicates a logical conjunction between variables. As a result, the compared variables must be true for the function to return a value of true.
Unlike the preceding examples, the two statements in Figure 3 are constructed much differently from each other. However, the truth values in the statement columns are still the same in all rows, so the statements are considered to be logically equivalent. Use the IIF function to show their logical equivalence within a single expression:
A ∨ (B ⋀ C) ⟺ (A ∨ B) ⋀ (A ∨ C)
In computing, logical equivalence is important in the design of digital circuits. If multiple circuits are logically equivalent, they have identical truth table values.
An engineer can use this information to identify the circuits that perform the desired logic using the fewest number of gates, which can help optimize operating efficiency, reliability and speed.
Learn how the relationship between humans and computers has evolved, see how logic games have advanced AI thinking and check out commonly used mathematical symbols and how they're used with sample expressions.
