What is bit (binary digit) in computing?
A bit (binary digit) is the smallest unit of data that a computer can process and store. It can have only one of two values: 0 or 1.
Bits are stored in memory through the use of capacitors that hold electrical charges. The charge determines the state of each bit which, in turn, determines the bit's value.
Importance of bits in the real world
Various combinations of bits -- combinations of 0s and 1s -- are used to represent numbers larger than 1. For example, an 8-bit binary number can represent 256 possible numbers from 0 to 255. A 16-bit binary number can represent even more numbers: 0 to 65,535. These combinations are important in computing because they determine which information is entered into and processed by a computing device.
A bit is always in one of two physical states, similar to an on/off light switch. The state is represented by a single binary value, usually 0 or 1. However, states might also be taken to mean yes/no, on/off or true/false. These binary values play an important role in many application areas, including the following:
- Computer programming.
- Telecommunications.
- Data analytics.
- Digital security.
In computer programming and data analysis, bits enable programmers to optimize code and create sophisticated algorithms for various applications like data processing. Programmers can manipulate individual bits to efficiently process large data sets and reduce memory usage even for complex data analysis/processing algorithms.
In telecommunications, data and audio/video signals are encoded and represented as multiple series of bits. These digital pieces of data are then transmitted over long distances through wireless or wired communication networks. The bit rate is an important concept in telecommunications because it impacts the speed and quality of the data transmission. It refers to the number of bits transmitted in a given time period, usually represented as the number of bits per second or some derivative, such as kilobits per second.
Finally, many data encryption and security methods rely on bits to safeguard data. Encryption keys are used to encrypt and decrypt data. Consisting of a series of bits, the keys are needed to convert plaintext data that anyone can read into encrypted characters that can only be decrypted and read by those who have the keys. Key holders are usually the data sender and the data recipient. In general, the longer the encryption key, i.e., the greater number of bits it contains, the stronger the encryption algorithm and the harder it is for unauthorized or malicious users to break it to read or steal the encrypted data.
Bits vs. bytes
Although a computer might be able to test and manipulate data at the bit level, most systems process and store data in bytes. A byte is a sequence of eight bits that are treated as a single unit. That said, there can be more or fewer than eight bits in a byte, depending on the data format or computer architecture in use.
References to a computer's memory and storage are always in terms of bytes.
For example, a storage device might be able to store 1 terabyte (TB) of data, which is equal to 1,000,000 megabytes (MB). To bring this into perspective, 1 MB equals 1 million bytes, or 8 million bits. That means a 1 TB drive can store more than 1 trillion data bytes (1 followed by 12 zeroes) or 8 trillion data bits (8 followed by 12 zeroes).
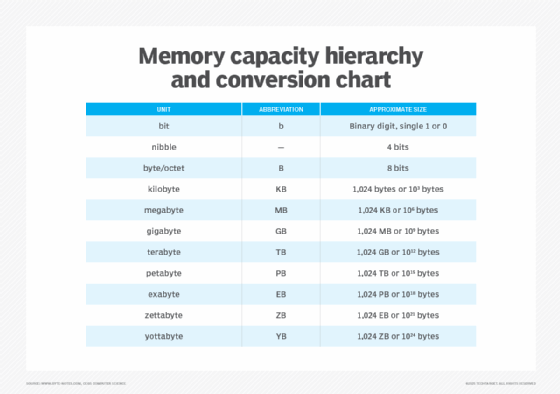
The term octet is sometimes used instead of byte, and the term nibble is occasionally used when referring to a 4-bit unit, although it's not as common as it once was. In addition, the term word is often used to describe two or more consecutive bytes. A word is usually 16, 32 or 64 bits long.
How a bit works
Each bit in a byte is assigned a specific value, which is referred to as the place value. A place value is assigned to each bit in a right-to-left pattern, starting with 1 and increasing the value by doubling it for each bit, as described in this table.
| Bit position (right to left) | Place value |
| Bit 1 |
1 |
| Bit 2 |
2 |
| Bit 3 |
4 |
| Bit 4 |
8 |
| Bit 5 |
16 |
| Bit 6 |
32 |
| Bit 7 |
64 |
| Bit 8 |
128 |
The place values of bits are used to determine the meaning and value of the byte as a whole, based on the individual bits. The place values indicate what character is associated with that byte.
To calculate this value, the place values associated with each 1 bit are added together. The place values associated with the 0 bits are not added into the byte total. This total corresponds to a character in the applicable character set, such as American Standard Code for Information Interchange (ASCII). ASCII is the most commonly used code to represent the 10 decimal digits (0 to 9), uppercase letters (A to Z), lowercase letters (a to z) and several special characters such as % and &.
A single byte, as a certain specific combination of 8 bits, can support up to 256 unique characters, starting with the 00000000 byte and ending with the 11111111 byte. The various combinations of bit patterns provide a range of 0 to 255, which means that each byte can support up to 256 unique bit patterns (up to 256 possible combinations can be used to transmit information).
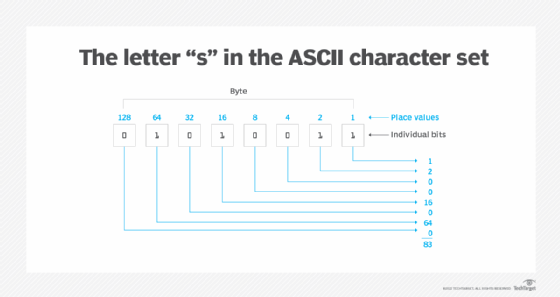
For example, the uppercase S in the ASCII character set is assigned the decimal value of 83, which is equivalent to the binary value of 01010011. This figure shows the S byte and the corresponding place values of each bit. The S byte includes four 1 bits and four 0 bits. When added together, the place values associated with 1 bits total 83, which corresponds to the decimal value assigned to the ASCII uppercase S character.
The lowercase s has different decimal and binary values than the uppercase S. The decimal value for lowercase s is 115. In byte terms, its value is 01110011.
Since 8-bit bytes can support only up to 256 unique characters in ASCII, other character sets have been developed to represent more characters. These character sets use multiple bytes per character. One is the Unicode Transformation Format (UTF) character set that uses between 1 and 4 bytes per character.
These differences notwithstanding, all character sets rely on the convention of 8 bits per byte, with each bit in either a 1 or 0 state.
What is a binary number system?
Because a binary number system uses only two bits to represent the numbers 0 and 1, various combinations of these bits are used to represent different numbers.
For example, the decimal number 1 is represented as 001, while 11 is represented as 1011.
Various operations can be performed on binary numbers, including the following:
- Binary addition.
- Binary subtraction.
- Binary multiplication.
- Binary division.
The binary system is also known as a base 2 system with a radix or base of 2 because it uses two unique digits to represent numbers. It is an important system because it is the foundation of all modern electronic and computing systems. Electronic circuits and logic gates are based on the binary system, as are programming languages, mobile devices, data storage devices, embedded systems and cryptography algorithms. The Internet Protocol (IP) also uses the system to route data packets.
The benefits of using a binary number system with two bits include simplicity, efficiency and compatibility among digital systems. Binary numbers are easy to work with as they only require two values (0 and 1) and can be used to represent a wide range of information, from simple binary data to complex digital signals.
Below are the other major number systems:
- Octal (Base 8).
- Decimal (Base 10).
- Hexadecimal (Base 16).
Memory is constructed from fundamental units known as bits and bytes. Grasping these concepts enhances storage efficiency and navigates the digital landscape. Learn about the different types of byte units in this explanatory article.