watt
What is a watt?
A watt (symbolized W) is the standard unit of power or radiant flux in the International System of Units (SI). It is derived from the SI base units kilogram (kg), meter (m) and second (s), all of which are constructed from the standard's defining constants. The watt is a measure of the rate of energy transfer over a unit of time, with one watt equal to one joule (J) per second:
W = J/s
A joule is the standard unit of energy or work in the SI standard, which defines the joule in terms of kilograms, meters and seconds:
J = kg∙m2∙s-2
A watt can also be expressed in these terms by combining the two previous formulas:
W = J/s = (kg∙m2∙s-2)/s = kg∙m2∙s-3
When applied to electromagnetic energy, the watt refers to the rate at which energy is radiated, absorbed or dissipated.
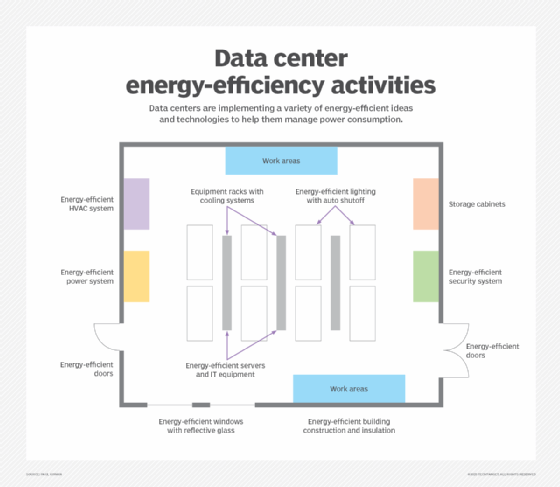
Understanding power and resource usage is the first step in learning what potential changes can make a difference for data centers, which are heavy users of electric power.
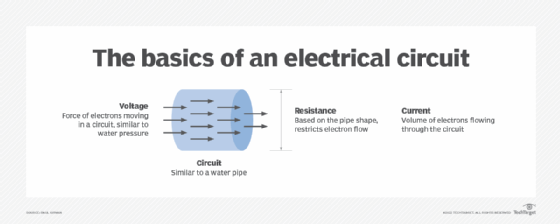
In an electrical circuit -- whether direct current (DC) or alternating current (AC) -- power is the product of the current and voltage. Current, which is measured in amperes (A), is the rate at which the energy flows. Voltage, which is measured in volts (V), is the difference in charge between two points. According to the SI standard, one volt is equal to one watt divided by one amp:
V = W/A
From this formula, we can come up with a formula for calculating watts by multiplying both sides by amps. This gives us the following formula, which indicates that one watt is equal to one volt times one amp:
W = VA
The watt is named after James Watt (1736-1819), a Scottish inventor and engineer. Although he patented several inventions, he is best known for his improvements to steam engine technology, which many consider instrumental in bringing about the Industrial Revolution.
Using Ohm's Law to measure power
Power is proportional to the ratio of the square of the voltage to the resistance, which is symbolized by R and measured in ohms (Ω). Consider a circuit in which the current, voltage and resistance are all constant. According to Ohm's Law, there is a proportional relationship between these three properties. The law states that voltage equals current (in amps) times resistance, as expressed in the following formula:
V = AR
We can combine this formula with the formula for wattage to incorporate resistance into our calculations. The first step is to revise the wattage formula by dividing both sides of the equation by V:
W = VA
A = W/V
The updated formula indicates that one amp equals one watt divided by one volt. The next step is to revise the Ohm's Law formula by dividing both sides of the equation by R:
V = AR
A = V/R
The updated formula indicates that one amp equals one volt divided by one ohm of resistance. Both revised formulas are now written so A is by itself on one side of the equation. We can now use these formulas to calculate wattage based on voltage and resistance. For this, we need to put the two formulas together, using the A value in both formulas:
W/V = A = V/R
W/V = V/R
W = V2/R
From this final formula, we can see that one watt equals one volt squared divided by one ohm of resistance, which demonstrates the proportional relationship between power, voltage and resistance. Power is also proportional to the product of the square of the current times the resistance. Using the same wattage and Ohm's Law formulas, we can also come up with a formula for calculating wattage based on current and resistance. This time the first step is to revise the wattage formula by dividing both sides of the equal sign by A:
W = VA
V = W/A
In this case, we don't need to revise the Ohm's Law formula because the V is already alone on one side of the equal sign. We need only put the two formulas together based on the V in both formulas:
W/A = V = AR
W/A = AR
W = A2R
These formulas can be useful for calculating watts in circuits when current, voltage and resistance are the primary considerations. However, they don't consider AC circuits that are also affected by reactance, which can result from inductance, capacitance or a combination of both. When reactance exists, the calculations become much more complex because multiple other factors must be considered.
In situations involving very high or very low power, prefix multipliers are commonly used to specify the wattage. For example, as power increases, 1 kilowatt (kW) can be used for 1,000 W, 1 megawatt (MW) for 106W and 1 gigawatt (GW) for 109 W. As power decreases, 1 milliwatt (mW) can be used for 0.001 W, 1 microwatt (µW) for 10-6 W and 1 nanowatt (nW) for 10-9 W.
Today, companies are responding to increasing pressure to make their data centers more environmentally friendly. Those able to do so can find rewards that transcend lower electrical costs.
