ohm
What is ohm?
The ohm is the standard unit of electrical resistance in the International System of Units (SI). It's one of the derived units defined in the SI standard, which means it's based directly or indirectly on the standard's fixed constants. The ohm is a measurement of resistance between two points of a conductor when a constant potential difference of one volt (V) is applied to those points and a current of one ampere (A) is produced. In simpler terms, it's the equivalent of one volt per one ampere (V/A). The ohm is represented by the Greek letter omega (Ω).
Ohms are sometimes expressed in power-of-10 multiples to accommodate large quantities. For example, one kiloohm is equal to 1,000 (103) ohms, and one megaohm is equal to 1,000 kiloohms or 1,000,000 (106) ohms. In addition, ohms can be expressed in smaller quantities, such as the microohm, which is 0.000001 (10-6) of a single ohm.
Calculating resistance in DC circuits
The ohm applies to both direct current (DC) and alternating current (AC). With DC, the electric charge flows in only one direction and doesn't oscillate back and forth like AC power. Three important quantities are used to measure a DC charge:
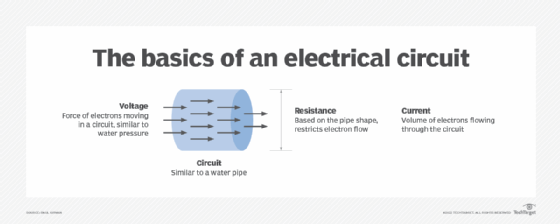
- Voltage (E). The difference in charge between two points, caused by the pressure that forces the current to flow. Voltage is measured in volts.
- Current (I). The rate at which the current flows. Current is measured in amperes, which are also referred to as amps.
- Resistance (R). The rate at which a material resists the current's flow. Resistance is measured in ohms.
These three quantities are directly related to each other, as demonstrated in Ohm's Law, which was introduced by Georg Simon Ohm (1789-1854), a German mathematician and physicist who experimented with electricity. The law states that there's a proportional relationship between voltage, current and resistance in an electrical circuit. Specifically, voltage equals current times resistance, or E = IR.
Using basic algebra, the formula can be rearranged to find any one of the three quantities, if two are known:
- Voltage: E = IR
- Current: I = E/R
- Resistance: R = E/I
The letter V is sometimes used to represent voltage rather than E, but the meaning is the same for the purpose of calculating quantities. In either case, the process is straightforward. For example, a circuit can be set up with a 9 V battery and a small lightbulb. The circuit currently produces a 0.5 A current. The following calculations can be used to determine the resistance created by the lightbulb:
R = E/I
R = 9 V/0.5 A
R = 18 Ω
A component on a DC circuit has a resistance of 1 Ω when a potential difference of 1 V produces a current of 1 A through the component, so a 9 V circuit with a 0.5 A current has a resistance of 18 Ω. In this example, however, the resistance is attributed entirely to the lightbulb, but a circuit's conductor (e.g., copper wire) can also be a source of resistance, as can other components.
Calculating resistance in AC circuits
Ohms are also used when measuring resistance in alternating current. Unlike DC power, AC oscillates in a sinusoidal waveform, and the electric current can reverse direction. For this reason, measuring resistance in AC circuits works differently from DC circuits because other components can inhibit a current's flow. Instead, the circuit's impedance must be measured, which considers not only resistance, but inductance and capacitance:
- Inductance (XL). The amount of impedance that can occur when an AC charge generates an electromagnetic field (EMF) that opposes the current. A component such as an inductor is often used to generate inductance.
- Capacitance (XC). The amount of electrical charge stored in the circuit. A component such as a capacitor is often used to generate capacitance.
Both inductance and capacitance are measured in ohms. Together, they're referred to as the circuit's reactance (X), which is also measured in ohms. Reactance is determined by using one of the following formulas to calculate the difference between inductance and capacitance:
- X = XL – XC
- X = XC – XL
The formula selected depends on whether inductance or capacitance is larger. The smaller amount is subtracted from the larger amount when determining the total reactance.

The principles of Ohm's Law can be used to calculate a circuit's electrical quantities, but the formula must be modified to consider impedance, which is represented by Z:
- Voltage: E = IZ
- Current: I = E/Z
- Impedance: Z = E/I
When an AC circuit contains resistance but no inductance or capacitance -- that is, no reactance -- it is treated as a DC -- so, simply plug in the resistance value for Z when calculating voltage or current. If there is reactance, the concept of root-mean-square (RMS) must be incorporated into the calculations. RMS is a mathematical method for defining the effective voltage or current of an AC sinusoidal wave. It's used to calculate a circuit's impedance:
Z= √(R2 + X2)
The formula requires that reactance (X) be calculated first, then square both resistance and reactance, add them together and find the square root of their sum. The value of Z can be plugged into the modified Ohm's Law formula. This approach can also be used when working with radiofrequency (RF) waves.
Explore how to create a more sustainable IT department, check out Power over Ethernet basics and learn about the types of batteries for IoT devices.
