quantum interference

What is quantum interference?

Quantum interference is when subatomic particles interact with and influence themselves and other particles while in a probabilistic superposition state. It can influence the probability of the outcomes when the quantum state is measured. Quantum interference, along with quantum entanglement, is essential to the operation of quantum computers.

Quantum interference is similar to interference in other types of waves. For example, imagine dropping two stones in a still pond of water creating two ripples, or sets of waves, in the pond. In some places, the high points, or crests, of two waves collide, resulting in a larger wave. In other places, the high point of one wave collides with the low point, or trough, of another wave, and the two cancel out.

In a quantum system, the particles exist as a probability wave of possible positions. These probability waves can interact so that, when the system is measured, some outcomes are more likely and other outcomes are less likely. This is known as an interference pattern. When the waves reinforce each other, it is called constructive interference. When they cancel each other out, it is called destructive interference.

Explaining quantum interference with the double-slit experiment

While quantum mechanics may appear intimidating, the double-slit experiment demonstrates many of its fundamental principles. Thomas Young performed the first double-slit experiment in 1801. It demonstrated light's wavelike behavior. It can be updated to demonstrate quantum mechanics principles and light's and electrons' dual wave-particle nature.

In the original double-slit experiment, a beam of coherent light, such as a laser or polarized light, is shone through a screen with two vertical slits in it. You may intuitively think that the resulting pattern of light on the other side of the screen would be like if there were two sources of light, with a single bright area where the two sources added together to be brighter and taper off at the edges. That is not what happens. Instead, alternating bands of light and dark areas are produced. Like the two ripples in the pond, the result is stronger in some places and weaker in other places, an interference pattern.

The double-slit experiment begins to show the effects of quantum mechanics when only a single photon is released at a time. If photographic film is placed on the other side of the screen and many photons are sent through, one at a time, what is the resulting pattern?

You may again intuitively think that, because only one photon is traveling, it must go through one slit or the other, and there is no photon from the other slit to interact with. And, therefore, there is no interference pattern. However, the results once again show an overall interference pattern.

The single photon somehow passed through both slits at the same time, interacting with or interfering with itself. This demonstrates that quantum interference occurred while the photon was in motion.

According to quantum mechanics, the single photon didn't split in half or go through both slits. Instead, it existed simultaneously at all possible points at the same time. This is known as superposition. The photon didn't finally decide where it was until it stuck to the photographic film. The superposition state, or quantum wave state, collapsed, and the photon became isolated at a single position.

This also helps to illustrate Heisenberg's uncertainty principle. While traveling, the particle had a velocity; therefore, its position could not be determined. Once it struck the film, its position became fixed, and its velocity became immeasurable.

The final phase of the double-slit experiment places a detector at one of the slits to determine which slit the photon travels through. The presence of the detector causes the location of the photon to be known, and therefore, the probability wave of the photon collapses, causing the photon to stop interfering with itself. No interference pattern is seen in the final output. This illustrates the principle that measuring a quantum system can change the outcome. When an incidental measurement causes an unwanted collapse or change of a quantum system, it is known as quantum decoherence.

The Mach-Zehnder interferometer is another experiment that shows the same effects as the double-slit experiment. It uses beam splitters and photon detectors to illustrate the superposition of single photons and the effect of measurement on a quantum system. It is more often used in mathematical explanations because it can be expressed with simpler algebra.

Quantum interference in quantum computers

Quantum interference is beneficial in quantum computers and used to perform calculations. It's important to note that quantum computers aren't always exact systems with definitive outcomes; instead, they employ probability to produce approximate or most likely outcomes. Quantum computers also calculate using qubit spin states or energy levels, not positions.

Qubits are initially set in a quantum computer. These qubits are then put into a superposition state. Quantum interference can then be used to program the system by operators or gates. The interference pushes the qubit system probability so that the correct answer is more likely and the incorrect answer is less likely.

Illustrating how quantum computers work

To illustrate how quantum computers work, imagine that the bits in a computer are coins, and heads and tails are one and zero. In a classical computer, you would lay the coins out on a table, and by moving and flipping the coins according to definitive rules, you would get a final output. This is an example of an idealized Turing machine.

In a quantum computer, though, you take the coins and the qubits and throw them in the air, where they spin. When the coins land, you check the heads and tails to get the answer. Of course, throwing coins randomly in the air and getting random answers is not useful, so quantum computers have more tricks up their sleeves.

Now, imagine the coins are magnets and can stay spinning in the air indefinitely. While in the air, you can do several things to control the coins:

• The coins can interact with each other, flipping one causes another to flip. This illustrates how quantum entanglement causes qubits to affect each other.
• You can place other magnets around the coins to cause certain outcomes to be more likely than others. This illustrates how quantum interference can be used to direct outcomes toward the desired output.
• You can use other magnets to cause certain coins to go through particular spins or have particular orientations. This is like how quantum gates cause changes in a qubit to program their state.

By combining entanglement, interference and gates, you can cause the coins to perform a calculation. When the coins land, they will most likely be in the correct outcome of heads and tails. But, because there is an element of probability present, you may only be 99.99% sure of the results, so you want to run the same process many times to increase your confidence.

This also illustrates the potential time savings of quantum computers. Imagine how long it will take to perform a calculation by hand using 128 coins as counters. Now, imagine if you could do the same calculation by throwing the 128 coins in the air and having them land in most likely the correct answer.

Real-world example of quantum interference use in a quantum computer

Grover's algorithm is a popular example of the superiority of quantum computers using quantum interference. It is a search function that can return the appropriate result from a random unsorted list by simultaneously evaluating all possible states at the same time. It uses a diffusion transform and a quantum oracle to influence the qubits over several iterations toward the correct result.

A classical computer would need to evaluate each result individually. If the list is N items long, a classical computer, on average, will take N/2 tries to find the answer, while Grover's algorithm on a quantum computer will take √N steps.

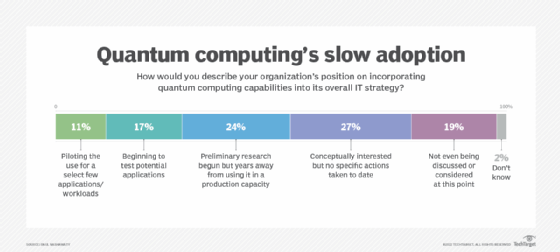
Grover's algorithm is mostly a teaching example and does not demonstrate true quantum supremacy yet. This is because it requires that the oracle be preprogrammed with some knowledge of the problem space. It also only provides a relatively modest quadratic improvement in speed over a classical computing approach, compared with other quantum computer algorithms that can produce exponentially faster results.

Still, it could be used against modern symmetric encryption schemes to speed up brute-force cracking attempts. This leads to the need for larger encryption keys now and the use of post-quantum cryptography.

Learn five quick quantum computing terms, explore seven future potential quantum computing uses, see the differences of classical vs. quantum computing and check out quantum computing challenges and opportunities.