phase
What is a phase?
In electronic signaling, a phase is the position of a wave at a point in time (instant) on a waveform cycle. It provides a measurement of exactly where the wave is positioned within its cycle, using either degrees (0-360) or radians (0-2π). One radian of a phase is equal to about 57.3 degrees. Engineers and technicians generally use degrees; physicists tend to use radians, although there are no hard-and-fast rules about usage.
A complete wave cycle is 360 degrees of a phase or 2π radians of a phase, as shown in Figure 1. The curving blue line represents the waveform, which is measured in terms of both amplitude and frequency. Amplitude indicates how far the wave deviates from its rest position as it alternates between positive peak amplitude and negative peak amplitude. Frequency is the number of cycles per second, with each cycle representing a unit of time. Frequency is measured in hertz (Hz) or one of its derivatives, such as kilohertz (kHz) or megahertz (MHz).
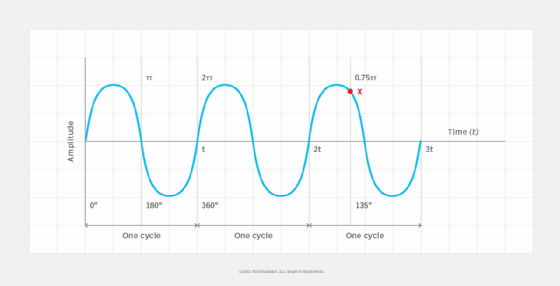
During any wave cycle, a wave's position can be identified by its phases. For example, the waveform in Figure 1 can be identified by these positions:
- The wave starts at the 0-degree phase (0 radians) and has no amplitude.
- The wave reaches positive peak amplitude at the 90-degree phase (0.5π radians).
- The wave returns to its amplitude rest position at the 180-degree phase (π radians).
- The wave reaches negative peak amplitude at the 270-degree phase (1.5π radians).
- The wave again returns to its amplitude rest position at the 360-degree phase (2π radians).
- The wave continues on to the next wave cycle, starting at 0 degrees with no amplitude.
Any point on the wave cycle can be identified by its phase. For example, in Figure 1, point X in the third cycle represents a phase of about 135 degrees (0.75π radians).
What are phase differences?
Often, the interest in phases has more to do with comparing two waves than it does with the individual wave. Phase difference, also called phase angle, is a measure in degrees of how much one wave leads another wave or lags behind that wave.
For example, Figure 2 shows two waves with the same amplitude and frequency but with different phase patterns. Wave A reaches its negative peak amplitude at 90 degrees, which is the same time that wave B reaches its positive peak amplitude. Both waves reach their rest positions at the same time, although they're moving in opposite directions. In this case, wave A lags behind wave B by 180 degrees, and wave B leads wave A by 180 degrees.
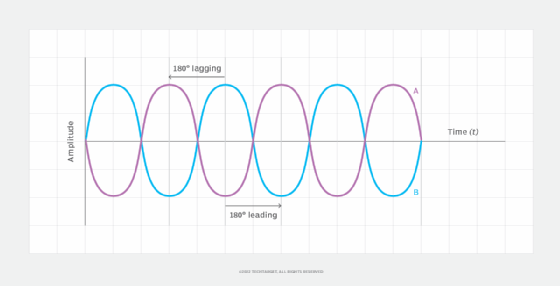
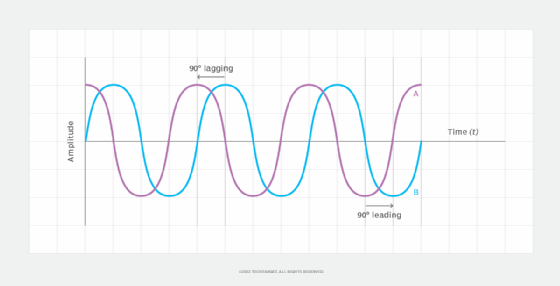
When two waves differ in phase by 180 degrees, whether -180 or +180, they are said to be in phase opposition. When two waves differ in phase by 90 degrees (-90 or +90), they are said to be in phase quadrature. Figure 3 shows two waves with the same amplitude and frequency but with a 90-degree phase difference. Wave A reaches its negative peak amplitude at 180 degrees -- at the same time that wave B reaches its rest point as it moves toward negative peak amplitude.
In some cases, it might be preferable to measure the phase difference in units of time rather than degrees or radians. Fortunately, converting a phase measurement is a fairly straightforward process. Because the time interval for one degree or radian of a phase is inversely proportional to the wave's frequency (f), you can use that frequency to calculate the time unit that corresponds to a single degree or radian. If working with degrees, you can use this formula:
tdeg = 1 / (360 x f)
The formula returns the time in seconds (tdeg) based on the inputted frequency in hertz. The 360 in the formula reflects the total number of degrees in a wave cycle, so the value returned by the equation corresponds to 1 degree of a phase out of the 360. If you're working with radians, you need to replace the 360 in the formula with 6.28 as shown here:
trad = 1 / (6.28 x f)
As with the previous formula, this one returns the time in seconds (trad) based on the inputted frequency. The 6.28 in the formula is the approximate number of radians in a wave cycle -- based on a total of 2π -- so the value returned by the equation corresponds to 1 radian out of the 6.28.
To better understand how these formulas work, consider a very low frequency (VLF) radio wave of 24 kHz (24,000 Hz). If you start with the degree formula, you can plug 24,000 into the equation in place of the f:
tdeg = 1 / (360 x f)
tdeg = 1 / (360 x 24,000)
tdeg = 1.15740741 × 10−7
The final line in the calculations shows the time unit for a frequency of 24 kHz, as it applies to 1 degree of a phase. If you are dealing with a 90-degree lag between waves, you can easily calculate the time unit for that lag by multiplying the results of the previous equation by 90:
90-degree lag = (1.15740741 × 10−7) x 90
90-degree lag = 1.04166667 × 10−5
Because this is still such a miniscule amount, you might want to convert the product to microseconds (µs). For this, you need only multiply the product by 1 million:
90-degree lag = (1.04166667 × 10−5) x 1000000
90-degree lag = 10.4166667 µs
From this, you can see that a 90-degree lag translates to about 10.42 µs, which converts to approximately 10,416.67 nanoseconds.
Why electronic signaling matters
It's useful to understand electronic signaling and digital logic, which is used to switch, combine or calculate signals, because the performance of a computer or network depends on proper signaling. While computer electrical signals are analog, they're usually called digital signals because they represent digital values (1 or 0). When signals travel over wires, they can pick up jitter, which is noise or cross-talk potentially capable of distorting or disrupting a signal. The receiving system can usually handle this -- make a 1 or 0 decision -- if jitter is minor. Moreover, if jitter isn't pervasive, error-correcting codes can fix it. But jitter is a consideration to account for.
See also: millimeter wave, wavelength, wave number, peak-to-peak , harmonic and wave polarization.
